4
Constants, Variables, and Data Types

Chapter 2 discussed the basic format for data in memory. Chapter 3 covered how a computer system physically organizes that data in memory. This chapter finishes the discussion by connecting the concept of data representation to its actual physical representation. As the title indicates, this chapter concerns itself with three main topics: constants, variables, and data structures. I do not assume that you’ve had a formal course in data structures, though such experience would be useful.
This chapter discusses how to declare and use constants, scalar variables, integers, data types, pointers, arrays, records/structures, and unions. You must master these subjects before going on to the next chapter. Declaring and accessing arrays, in particular, seem to present a multitude of problems to beginning assembly language programmers. However, the rest of this text depends on your understanding of these data structures and their memory representation. Do not try to skim over this material with the expectation that you will pick it up as you need it later. You will need it right away, and trying to learn this material along with later material will only confuse you more.
4.1 The imul Instruction
This chapter introduces arrays and other concepts that will require the expansion of your x86-64 instruction set knowledge. In particular, you will need to learn how to multiply two values; hence, this section looks at the imul (integer multiply) instruction.
The imul instruction has several forms. This section doesn’t cover all of them, just the ones that are useful for array calculations (for the remaining imul instructions, see “Arithmetic Expressions” in Chapter 6). The imul variants of interest right now are as follows:
; The following computes destreg = destreg * constant:
imul destreg16, constant
imul destreg32, constant
imul destreg64, constant32
; The following computes dest = src * constant:
imul destreg16, srcreg16, constant
imul destreg16, srcmem16, constant
imul destreg32, srcreg32, constant
imul destreg32, srcmem32, constant
imul destreg64, srcreg64, constant32
imul destreg64, srcmem64, constant32
; The following computes dest = destreg * src:
imul destreg16, srcreg16
imul destreg16, srcmem16
imul destreg32, srcreg32
imul destreg32, srcmem32
imul destreg64, srcreg64
imul destreg64, srcmem64Note that the syntax of the imul instruction is different from that of the add and sub instructions. In particular, the destination operand must be a register (add and sub both allow a memory operand as a destination). Also note that imul allows three operands when the last operand is a constant. Another important difference is that the imul instruction allows only 16-, 32-, and 64-bit operands; it does not multiply 8-bit operands. Finally, as is true for most instructions that support the immediate addressing mode, the CPU limits constant sizes to 32 bits. For 64-bit operands, the x86-64 will sign-extend the 32-bit immediate constant to 64 bits.
imul computes the product of its specified operands and stores the result into the destination register. If an overflow occurs (which is always a signed overflow, because imul multiplies only signed integer values), then this instruction sets both the carry and overflow flags. imul leaves the other condition code flags undefined (so, for example, you cannot meaningfully check the sign flag or the zero flag after executing imul).
4.2 The inc and dec Instructions
As several examples up to this point have indicated, adding or subtracting 1 from a register or memory location is a very common operation. In fact, these operations are so common that Intel’s engineers included a pair of instructions to perform these specific operations: inc (increment) and dec (decrement).
The inc and dec instructions use the following syntax:
inc mem/reg
dec mem/regThe single operand can be any legal 8-, 16-, 32-, or 64-bit register or memory operand. The inc instruction will add 1 to the specified operand, and the dec instruction will subtract 1 from the specified operand.
These two instructions are slightly shorter than the corresponding add or sub instructions (their encoding uses fewer bytes). There is also one slight difference between these two instructions and the corresponding add or sub instructions: they do not affect the carry flag.
4.3 MASM Constant Declarations
MASM provides three directives that let you define constants in your assembly language programs.1 Collectively, these three directives are known as equates. You’ve already seen the most common form:
symbol = constant_expressionFor example:
MaxIndex = 15Once you declare a symbolic constant in this manner, you may use the symbolic identifier anywhere the corresponding literal constant is legal. These constants are known as manifest constants—symbolic representations that allow you to substitute the literal value for the symbol anywhere in the program.
Contrast this with .const variables; a .const variable is certainly a constant value because you cannot change its value at runtime. However, a memory location is associated with a .const variable; the operating system, not the MASM compiler, enforces the read-only attribute. Although it will certainly crash your program when it runs, it is perfectly legal to write an instruction like mov ReadOnlyVar, eax. On the other hand, it is no more legal to write mov MaxIndex, eax (using the preceding declaration) than it is to write mov 15, eax. In fact, both statements are equivalent because the compiler substitutes 15 for MaxIndex whenever it encounters this manifest constant.
Constant declarations are great for defining “magic” numbers that might possibly change during program modification. Most of the listings throughout this book have used manifest constants like nl (newline), maxLen, and NULL.
In addition to the = directive, MASM provides the equ directive:
symbol equ constant_expressionWith a couple exceptions, these two equate directives do the same thing: they define a manifest constant, and MASM will substitute the constant_expression value wherever the symbol appears in the source file.
The first difference between the two is that MASM allows you to redefine symbols that use the = directive. Consider the following code snippet:
maxSize = 100
Code that uses maxSize, expecting it to be 100
maxSize = 256
Code that uses maxSize, expecting it to be 256You might question the term constant when it’s pretty clear in this example that maxSize’s value changes at various points in the source file. However, note that while maxSize’s value does change during assembly, at runtime the particular literal constant (100 or 256 in this example) can never change.
You cannot redefine the value of a constant you declare with an equ directive (at runtime or assembly time). Any attempt to redefine an equ symbol results in a symbol redefinition error from MASM. So if you want to prevent the accidental redefinition of a constant symbol in your source file, you should use the equ directive rather than the = directive.
Another difference between the = and equ directives is that constants you define with = must be representable as a 64-bit (or smaller) integer. Short character strings are legal as = operands, but only if they have eight or fewer characters (which would fit into a 64-bit value). Equates using equ have no such limitation.
Ultimately, the difference between = and equ is that the = directive computes the value of a numeric expression and saves that value to substitute wherever that symbol appears in the program. The equ directive, if its operand can be reduced to a numeric value, will work the same way. However, if the equ operand cannot be converted to a numeric value, then the equ directive will save its operand as textual data and substitute that textual data in place of the symbol.
Because of the numeric/text processing, equ can get confused on occasion by its operand. Consider the following example:
SomeStr equ "abcdefgh"
.
.
.
memStr byte SomeStrMASM will report an error (initializer magnitude too large for specified size or something similar) because a 64-bit value (obtained by creating an integer value from the eight characters abcdefgh) will not fit into a byte variable. However, if we add one more character to the string, MASM will gladly accept this:
SomeStr equ "abcdefghi"
.
.
.
memStr byte SomeStrThe difference between these two examples is that in the first case, MASM decides that it can represent the string as a 64-bit integer, so the constant is a quad-word constant rather than a string of characters. In the second example, MASM cannot represent the string of characters as an integer, so it treats the operand as a text operand rather than a numeric operand. When MASM does a textual substitution of the string abcdefghi for memStr in the second example, MASM assembles the code properly because strings are perfectly legitimate operands for the byte directive.
Assuming you really want MASM to treat a string of eight characters or fewer as a string rather than as an integer value, there are two solutions. The first is to surround the operand with text delimiters. MASM uses the symbols < and > as text delimiters in an equ operand field. So, you could use the following code to solve this problem:
SomeStr equ <"abcdefgh">
.
.
.
memStr byte SomeStrBecause the equ directive’s operand can be somewhat ambiguous at times, Microsoft introduced a third equate directive, textequ, to use when you want to create a text equate. Here’s the current example using a text equate:
SomeStr textequ <"abcdefgh">
.
.
.
memStr byte SomeStrNote that textequ operands must always use the text delimiters (< and >) in the operand field.
Whenever MASM encounters a symbol defined with the text directive in a source file, it will immediately substitute the text associated with that directive for the identifier. This is somewhat similar to the C/C++ #define macro (except you don’t get to specify any parameters). Consider the following example:
maxCnt = 10
max textequ <maxCnt>
max = max+1MASM substitutes maxCnt for max throughout the program (after the textequ declaring max). In the third line of this example, this substitution yields the statement:
maxCnt = maxCnt+1Thereafter in the program, MASM will substitute the value 11 everywhere it sees the symbol maxCnt. Whenever MASM sees max after that point, it will substitute maxCnt, and then it will substitute 11 for maxCnt.
You could even use MASM text equates to do something like the following:
mv textequ <mov>
.
.
.
mv rax,0MASM will substitute mov for mv and compile the last statement in this sequence into a mov instruction. Most people would consider this a huge violation of assembly language programming style, but it’s perfectly legal.
4.3.1 Constant Expressions
Thus far, this chapter has given the impression that a symbolic constant definition consists of an identifier, an optional type, and a literal constant. Actually, MASM constant declarations can be a lot more sophisticated than this because MASM allows the assignment of a constant expression, not just a literal constant, to a symbolic constant. The generic constant declaration takes one of the following two forms:
identifier = constant_expression
identifier equ constant_expressionConstant (integer) expressions take the familiar form you’re used to in high-level languages like C/C++ and Python. They may contain literal constant values, previously declared symbolic constants, and various arithmetic operators.
The constant expression operators follow standard precedence rules (similar to those in C/C++); you may use the parentheses to override the precedence if necessary. In general, if the precedence isn’t obvious, use parentheses to exactly state the order of evaluation. Table 4-1 lists the arithmetic operators MASM allows in constant (and address) expressions.
Table 4-1: Operations Allowed in Constant Expressions
| Arithmetic operators | |
- (unary negation) |
Negates the expression immediately following -. |
* |
Multiplies the integer or real values around the asterisk. |
/ |
Divides the left integer operand by the right integer operand, producing an integer (truncated) result. |
mod |
Divides the left integer operand by the right integer operand, producing an integer remainder. |
/ |
Divides the left numeric operand by the second numeric operand, producing a floating-point result. |
+ |
Adds the left and right numeric operands. |
- |
Subtracts the right numeric operand from the left numeric operand. |
[] |
expr1[expr2] computes the sum of expr1 + expr2. |
| Comparison operators | |
EQ |
Compares left operand with right operand. Returns true if equal.* |
NE |
Compares left operand with right operand. Returns true if not equal. |
LT |
Returns true if left operand is less than right operand. |
LE |
Returns true if left operand is ≤ right operand. |
GT |
Returns true if left operand is greater than right operand. |
GE |
Returns true if left operand is ≥ right operand. |
| Logical operators** | |
AND |
For Boolean operands, returns the logical AND of the two operands. |
OR |
For Boolean operands, returns the logical OR of the two operands. |
NOT |
For Boolean operands, returns the logical negation (inverse). |
| Unary operators | |
HIGH |
Returns the HO byte of the LO 16 bits of the following expression. |
HIGHWORD |
Returns the HO word of the LO 32 bits of the following expression. |
HIGH32 |
Returns the HO 32 bits of the 64-bit expression following the operator. |
LENGTHOF |
Returns the number of data elements of the variable name following the operator. |
LOW |
Returns the LO byte of the expression following the operator. |
LOWWORD |
Returns the LO word of the expression following the operator. |
LOW32 |
Returns the LO dword of the expression following the operator. |
OFFSET |
Returns the offset into its respective section for the symbol following the operator. |
OPATTR |
Returns the attributes of the expression following the operator. The attributes are returned as a bit map with the following meanings: bit 0: There is a code label in the expression. bit 1: The expression is relocatable. bit 2: The expression is a constant expression. bit 3: The expression uses direct addressing. bit 4: The expression is a register. bit 5: The expression contains no undefined symbols. bit 6: The expression is a stack-segment memory expression. bit 7: The expression references an external label. bits 8–11: Language type (probably 0 for 64-bit code). |
SIZE |
Returns the size, in bytes, of the first initializer in a symbol’s declaration. |
SIZEOF |
Returns the size, in bytes, allocated for a given symbol. |
THIS |
Returns an address expression equal to the value of the current program counter within a section. Must include type after this; for example, this byte. |
$ |
Synonym for this. |
4.3.2 this and $ Operators
The last two operators in Table 4-1 deserve special mention. The this and $ operands (they are roughly synonyms for one another) return the current offset into the section containing them. The current offset into the section is known as the location counter (see “How MASM Allocates Memory for Variables” in Chapter 3). Consider the following:
someLabel equ $This sets the label’s offset to the current location in the program. The type of the symbol will be statement label (for example, proc). Typically, people use the $ operator for branch labels (and advanced features). For example, the following creates an infinite loop (effectively locking up the CPU):
jmp $ ; "$" is equivalent to the address of the jmp instrYou can also use instructions like this to skip a fixed number of bytes ahead (or behind) in the source file:
jmp $+5 ; Skip to a position 5 bytes beyond the jmpFor the most part, creating operands like this is crazy because it depends on knowing the number of bytes of machine code each machine instruction compiles into. Obviously, this is an advanced operation and not recommended for beginning assembly language programmers (it’s even hard to recommend for most advanced assembly language programmers).
One practical use of the $ operator (and probably its most common use) is to compute the size of a block of data declarations in the source file:
someData byte 1, 2, 3, 4, 5
sizeSomeData = $-someDataThe address expression $-someData computes the current offset minus the offset of someData in the current section. In this case, this produces 5, the number of bytes in the someData operand field. In this simple example, you’re probably better off using the sizeof someData expression. This also returns the number of bytes required for the someData declaration. However, consider the following statements:
someData byte 1, 2, 3, 4, 5
byte 6, 7, 8, 9, 0
sizeSomeData = $-someDataIn this case, sizeof someData still returns 5 (because it returns only the length of the operands attached to someData), whereas sizeSomeData is set to 10.
If an identifier appears in a constant expression, that identifier must be a constant identifier that you have previously defined in your program in the equate directive. You may not use variable identifiers in a constant expression; their values are not defined at assembly time when MASM evaluates the constant expression. Also, don’t confuse compile-time and runtime operations:
; Constant expression, computed while MASM
; is assembling your program:
x = 5
y = 6
Sum = x + y
; Runtime calculation, computed while your program
; is running, long after MASM has assembled it:
mov al, x
add al, yThe this operator differs from the $ operator in one important way: the $ has a default type of statement label. The this operator, on the other hand, allows you to specify a type. The syntax for the this operator is the following:
this typewhere type is one of the usual data types (byte, sbyte, word, sword, and so forth). Therefore, this proc is what is directly equivalent to $. Note that the following two MASM statements are equivalent:
someLabel label byte
someLabel equ this byte4.3.3 Constant Expression Evaluation
MASM immediately interprets the value of a constant expression during assembly. It does not emit any machine instructions to compute x + y in the constant expression of the example in the previous section. Instead, it directly computes the sum of these two constant values. From that point forward in the program, MASM associates the value 11 with the constant Sum just as if the program had contained the statement Sum = 11 rather than Sum = x + y. On the other hand, MASM does not precompute the value 11 in AL for the mov and add instructions in the previous section; it faithfully emits the object code for these two instructions, and the x86-64 computes their sum when the program is run (sometime after the assembly is complete).
In general, constant expressions don’t get very sophisticated in assembly language programs. Usually, you’re adding, subtracting, or multiplying two integer values. For example, the following set of equates defines a set of constants that have consecutive values:
TapeDAT = 0
Tape8mm = TapeDAT + 1
TapeQIC80 = Tape8mm + 1
TapeTravan = TapeQIC80 + 1
TapeDLT = TapeTravan + 1These constants have the following values: TapeDAT = 0, Tape8mm = 1, TapeQIC80 = 2, TapeTravan = 3, and TapeDLT = 4. This example, by the way, demonstrates how you would create a list of enumerated data constants in MASM.
4.4 The MASM typedef Statement
Let’s say that you do not like the names that MASM uses for declaring byte, word, dword, real4, and other variables. Let’s say that you prefer Pascal’s naming convention or perhaps C’s naming convention. You want to use terms like integer, float, double, or whatever. If MASM were Pascal, you could redefine the names in the type section of the program. With C, you could use a typedef statement to accomplish the task. Well, MASM, like C/C++, has its own type statement that also lets you create aliases of these names. The MASM typedef statement takes the following form:
new_type_name typedef existing_type_nameThe following example demonstrates how to set up some names in your MASM programs that are compatible with C/C++ or Pascal:
integer typedef sdword
float typedef real4
double typedef real8
colors typedef byteNow you can declare your variables with more meaningful statements like these:
.data
i integer ?
x float 1.0
HouseColor colors ?If you program in Ada, C/C++, or FORTRAN (or any other language, for that matter), you can pick type names you’re more comfortable with. Of course, this doesn’t change how the x86-64 or MASM reacts to these variables one iota, but it does let you create programs that are easier to read and understand because the type names are more indicative of the actual underlying types. One warning for C/C++ programmers: don’t get too excited and go off and define an int data type. Unfortunately, int is an x86-64 machine instruction (interrupt), and therefore this is a reserved word in MASM.
4.5 Type Coercion
Although MASM is fairly loose when it comes to type checking, MASM does ensure that you specify appropriate operand sizes to an instruction. For example, consider the following (incorrect) program in Listing 4-1.
; Listing 4-1
; Type checking errors.
option casemap:none
nl = 10 ; ASCII code for newline
.data
i8 sbyte ?
i16 sword ?
i32 sdword ?
i64 sqword ?
.code
; Here is the "asmMain" function.
public asmMain
asmMain proc
mov eax, i8
mov al, i16
mov rax, i32
mov ax, i64
ret ; Returns to caller
asmMain endp
endListing 4-1: MASM type checking
MASM will generate errors for these four mov instructions because the operand sizes are incompatible. The mov instruction requires both operands to be the same size. The first instruction attempts to move a byte into EAX, the second instruction attempts to move a word into AL, and the third instruction attempts to move a double word into RAX. The fourth instruction attempts to move a qword into AX. Here’s the output from the compiler when you attempt to assemble this file:
C:\>ml64 /c listing4-1.asm
Microsoft (R) Macro Assembler (x64) Version 14.15.26730.0
Copyright (C) Microsoft Corporation. All rights reserved.
Assembling: listing4-1.asm
listing4-1.asm(24) : error A2022:instruction operands must be the same size
listing4-1.asm(25) : error A2022:instruction operands must be the same size
listing4-1.asm(26) : error A2022:instruction operands must be the same size
listing4-1.asm(27) : error A2022:instruction operands must be the same sizeWhile this is a good feature in MASM,2 sometimes it gets in the way. Consider the following code fragments:
.data
byte_values label byte
byte 0, 1
.
.
.
mov ax, byte_valuesIn this example, let’s assume that the programmer really wants to load the word starting at the address of byte_values into the AX register because they want to load AL with 0, and AH with 1, by using a single instruction (0 is held in the LO memory byte, and 1 is held in the HO memory byte). MASM will refuse, claiming a type mismatch error (because byte_values is a byte object and AX is a word object).
The programmer could break this into two instructions, one to load AL with the byte at address byte_values and the other to load AH with the byte at address byte_values[1]. Unfortunately, this decomposition makes the program slightly less efficient (which was probably the reason for using the single mov instruction in the first place). To tell MASM that we know what we’re doing and we want to treat the byte_values variable as a word object, we can use type coercion.
Type coercion is the process of telling MASM that you want to treat an object as an explicit type, regardless of its actual type.3 To coerce the type of a variable, you use the following syntax:
new_type_name ptr address_expressionThe new_type_name item is the new type you wish to associate with the memory location specified by address_expression. You may use this coercion operator anywhere a memory address is legal. To correct the previous example, so MASM doesn’t complain about type mismatches, you would use the following statement:
mov ax, word ptr byte_valuesThis instruction tells MASM to load the AX register with the word starting at address byte_values in memory. Assuming byte_values still contains its initial value, this instruction will load 0 into AL and 1 into AH.
Table 4-2 lists all the MASM type-coercion operators.
Table 4-2: MASM Type-Coercion Operators
| Directive | Meaning |
byte ptr |
Byte (unsigned 8-bit) value |
sbyte ptr |
Signed 8-bit integer value |
word ptr |
Unsigned 16-bit (word) value |
sword ptr |
Signed 16-bit integer value |
dword ptr |
Unsigned 32-bit (double-word) value |
sdword ptr |
Signed 32-bit integer value |
qword ptr |
Unsigned 64-bit (quad-word) value |
sqword ptr |
Signed 64-bit integer value |
tbyte ptr |
Unsigned 80-bit (10-byte) value |
oword ptr |
128-bit (octal-word) value |
xmmword ptr |
128-bit (octal-word) value—same as oword ptr |
ymmword ptr |
256-bit value (for use with AVX YMM registers) |
zmmword ptr |
512-bit value (for use with AVX-512 ZMM registers) |
real4 ptr |
Single-precision (32-bit) floating-point value |
real8 ptr |
Double-precision (64-bit) floating-point value |
real10 ptr |
Extended-precision (80-bit) floating-point value |
Type coercion is necessary when you specify an anonymous variable as the operand to an instruction that directly modifies memory (for example, neg, shl, not, and so on). Consider the following statement:
not [rbx]MASM will generate an error on this instruction because it cannot determine the size of the memory operand. The instruction does not supply sufficient information to determine whether the program should invert the bits in the byte pointed at by RBX, the word pointed at by RBX, the double word pointed at by RBX, or the quad word pointed at by RBX. You must use type coercion to explicitly specify the size of anonymous references with these types of instructions:
not byte ptr [rbx]
not dword ptr [rbx]Consider the following statement (where byteVar is an 8-bit variable):
mov dword ptr byteVar, eaxWithout the type-coercion operator, MASM complains about this instruction because it attempts to store a 32-bit register in an 8-bit memory location. Beginning programmers, wanting their programs to assemble, may take a shortcut and use the type-coercion operator, as shown in this instruction; this certainly quiets the assembler—it will no longer complain about a type mismatch—so the beginning programmers are happy.
However, the program is still incorrect; the only difference is that MASM no longer warns you about your error. The type-coercion operator does not fix the problem of attempting to store a 32-bit value into an 8-bit memory location—it simply allows the instruction to store a 32-bit value starting at the address specified by the 8-bit variable. The program still stores 4 bytes, overwriting the 3 bytes following byteVar in memory.
This often produces unexpected results, including the phantom modification of variables in your program.4 Another, rarer possibility is for the program to abort with a general protection fault, if the 3 bytes following byteVar are not allocated in real memory or if those bytes just happen to fall in a read-only section of memory. The important thing to remember about the type-coercion operator is this: if you cannot exactly state the effect this operator has, don’t use it.
Also keep in mind that the type-coercion operator does not perform any translation of the data in memory. It simply tells the assembler to treat the bits in memory as a different type. It will not automatically extend an 8-bit value to 32 bits, nor will it convert an integer to a floating-point value. It simply tells the compiler to treat the bit pattern of the memory operand as a different type.
4.6 Pointer Data Types
You’ve probably experienced pointers firsthand in the Pascal, C, or Ada programming languages, and you’re probably getting worried right now. Almost everyone has a bad experience when they first encounter pointers in a high-level language. Well, fear not! Pointers are actually easier to deal with in assembly language than in high-level languages.
Besides, most of the problems you had with pointers probably had nothing to do with pointers but rather with the linked list and tree data structures you were trying to implement with them. Pointers, on the other hand, have many uses in assembly language that have nothing to do with linked lists, trees, and other scary data structures. Indeed, simple data structures like arrays and records often involve the use of pointers. So, if you have some deep-rooted fear about pointers, forget everything you know about them. You’re going to learn how great pointers really are.
Probably the best place to start is with the definition of a pointer. A pointer is a memory location whose value is the address of another memory location. Unfortunately, high-level languages like C/C++ tend to hide the simplicity of pointers behind a wall of abstraction. This added complexity (which exists for good reason, by the way) tends to frighten programmers because they don’t understand what’s going on.
To illuminate what’s really happening, consider the following array declaration in Pascal:
M: array [0..1023] of integer;Even if you don’t know Pascal, the concept here is pretty easy to understand. M is an array with 1024 integers in it, indexed from M[0] to M[1023]. Each one of these array elements can hold an integer value that is independent of all the others. In other words, this array gives you 1024 different integer variables, each of which you refer to by number (the array index) rather than by name.
If you encounter a program that has the statement M[0] := 100;, you probably won’t have to think at all about what is happening with this statement. It is storing the value 100 into the first element of the array M. Now consider the following two statements:
i := 0; (Assume "i" is an integer variable)
M [i] := 100;You should agree, without too much hesitation, that these two statements perform the same operation as M[0] := 100;. Indeed, you’re probably willing to agree that you can use any integer expression in the range 0 to 1023 as an index into this array. The following statements still perform the same operation as our single assignment to index 0:
i := 5; (Assume all variables are integers)
j := 10;
k := 50;
m [i*j-k] := 100;“Okay, so what’s the point?” you’re probably thinking. “Anything that produces an integer in the range 0 to 1023 is legal. So what?” Okay, how about the following:
M [1] := 0;
M [M [1]] := 100;Whoa! Now that takes a few moments to digest. However, if you take it slowly, it makes sense, and you’ll discover that these two instructions perform the same operation you’ve been doing all along. The first statement stores 0 into array element M[1]. The second statement fetches the value of M[1], which is an integer so you can use it as an array index into M, and uses that value (0) to control where it stores the value 100.
If you’re willing to accept this as reasonable—perhaps bizarre, but usable nonetheless—then you’ll have no problems with pointers. Because M[1] is a pointer! Well, not really, but if you were to change M to memory and treat this array as all of memory, this is the exact definition of a pointer: a memory location whose value is the address (or index, if you prefer) of another memory location. Pointers are easy to declare and use in an assembly language program. You don’t even have to worry about array indices or anything like that.
4.6.1 Using Pointers in Assembly Language
A MASM pointer is a 64-bit value that may contain the address of another variable. If you have a dword variable p that contains 1000_0000h, then p “points” at memory location 1000_0000h. To access the dword that p points at, you could use code like the following:
mov rbx, p ; Load RBX with the value of pointer p
mov rax, [rbx] ; Fetch the data that p points atBy loading the value of p into RBX, this code loads the value 1000_0000h into RBX (assuming p contains 1000_0000h). The second instruction loads the RAX register with the qword starting at the location whose offset appears in RBX. Because RBX now contains 1000_0000h, this will load RAX from locations 1000_0000h through 1000_0007h.
Why not just load RAX directly from location 1000_0000h by using an instruction like mov rax, mem (assuming mem is at address 1000_0000h)? Well, there are several reasons. But the primary reason is that this mov instruction always loads RAX from location mem. You cannot change the address from where it loads RAX. The former instructions, however, always load RAX from the location where p is pointing. This is easy to change under program control. In fact, the two instructions mov rax, offset mem2 and mov p, rax will cause those previous two instructions to load RAX from mem2 the next time they execute. Consider the following code fragment:
mov rax, offset i
mov p, rax
.
.
. ; Code that sets or clears the carry flag.
jc skipSetp
mov rax, offset j
mov p, rax
.
.
.
skipSetp:
mov rbx, p ; Assume both code paths wind up
mov rax, [rbx] ; down hereThis short example demonstrates two execution paths through the program. The first path loads the variable p with the address of the variable i. The second path through the code loads p with the address of the variable j. Both execution paths converge on the last two mov instructions that load RAX with i or j depending on which execution path was taken. In many respects, this is like a parameter to a procedure in a high-level language like Swift. Executing the same instructions accesses different variables depending on whose address (i or j) winds up in p.
4.6.2 Declaring Pointers in MASM
Because pointers are 64 bits long, you could use the qword type to allocate storage for your pointers. However, rather than use qword declarations, an arguably better approach is to use typedef to create a pointer type:
.data
pointer typedef qword
b byte ?
d dword ?
pByteVar pointer b
pDWordVar pointer dThis example demonstrates that it is possible to initialize as well as declare pointer variables in MASM. Note that you may specify addresses of static variables (.data, .const, and .data? objects) in the operand field of a qword/pointer directive, so you can initialize only pointer variables with the addresses of static objects.
4.6.3 Pointer Constants and Pointer Constant Expressions
MASM allows very simple constant expressions wherever a pointer constant is legal. Pointer constant expressions take one of the three following forms:5
offset StaticVarName [PureConstantExpression]
offset StaticVarName + PureConstantExpression
offset StaticVarName - PureConstantExpressionThe PureConstantExpression term is a numeric constant expression that does not involve any pointer constants. This type of expression produces a memory address that is the specified number of bytes before or after (- or +, respectively) the StaticVarName variable in memory. Note that the first two forms shown here are semantically equivalent; both return a pointer constant whose address is the sum of the static variable and the constant expression.
Because you can create pointer constant expressions, it should come as no surprise to discover that MASM lets you define manifest pointer constants by using equates. The program in Listing 4-2 demonstrates how you can do this.
; Listing 4-2
; Pointer constant demonstration.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 4-2", 0
fmtStr byte "pb's value is %ph", nl
byte "*pb's value is %d", nl, 0
.data
b byte 0
byte 1, 2, 3, 4, 5, 6, 7
pb textequ <offset b[2]>
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 48
lea rcx, fmtStr
mov rdx, pb
movzx r8, byte ptr [rdx]
call printf
add rsp, 48
ret ; Returns to caller
asmMain endp
endListing 4-2: Pointer constant expressions in a MASM program
Here’s the assembly and execution of this code:
C:\>build listing4-2
C:\>echo off
Assembling: listing4-2.asm
c.cpp
C:\>listing4-2
Calling Listing 4-2:
pb's value is 00007FF6AC381002h
*pb's value is 2
Listing 4-2 terminatedNote that the address printed may vary on different machines and different versions of Windows.
4.6.4 Pointer Variables and Dynamic Memory Allocation
Pointer variables are the perfect place to store the return result from the C Standard Library malloc() function. This function returns the address of the storage it allocates in the RAX register; therefore, you can store the address directly into a pointer variable with a single mov instruction immediately after a call to malloc(). Listing 4-3 demonstrates calls to the C Standard Library malloc() and free() functions.
; Listing 4-3
; Demonstration of calls
; to C standard library malloc
; and free functions.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 4-3", 0
fmtStr byte "Addresses returned by malloc: %ph, %ph", nl, 0
.data
ptrVar qword ?
ptrVar2 qword ?
.code
externdef printf:proc
externdef malloc:proc
externdef free:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 48
; C standard library malloc function.
; ptr = malloc(byteCnt);
mov rcx, 256 ; Allocate 256 bytes
call malloc
mov ptrVar, rax ; Save pointer to buffer
mov rcx, 1024 ; Allocate 1024 bytes
call malloc
mov ptrVar2, rax ; Save pointer to buffer
lea rcx, fmtStr
mov rdx, ptrVar
mov r8, rax ; Print addresses
call printf
; Free the storage by calling
; C standard library free function.
; free(ptrToFree);
mov rcx, ptrVar
call free
mov rcx, ptrVar2
call free
add rsp, 48
ret ; Returns to caller
asmMain endp
endListing 4-3: Demonstration of malloc() and free() calls
Here’s the output I obtained when building and running this program. Note that the addresses that malloc() returns may vary by system, by operating system version, and for other reasons. Therefore, you will likely get different numbers than I obtained on my system.
C:\>build listing4-3
C:\>echo off
Assembling: listing4-3.asm
c.cpp
C:\>listing4-3
Calling Listing 4-3:
Addresses returned by malloc: 0000013B2BC43AD0h, 0000013B2BC43BE0h
Listing 4-3 terminated4.6.5 Common Pointer Problems
Programmers encounter five common problems when using pointers. Some of these errors will cause your programs to immediately stop with a diagnostic message; other problems are subtler, yielding incorrect results without otherwise reporting an error or simply affecting the performance of your program without displaying an error. These five problems are as follows:
- Using an uninitialized pointer
- Using a pointer that contains an illegal value (for example, NULL)
- Continuing to use
malloc()’d storage after that storage has been freed - Failing to
free()storage once the program is finished using it - Accessing indirect data by using the wrong data type
The first problem is using a pointer variable before you have assigned a valid memory address to the pointer. Beginning programmers often don’t realize that declaring a pointer variable reserves storage only for the pointer itself; it does not reserve storage for the data that the pointer references. The short program in Listing 4-4 demonstrates this problem (don’t try to compile and run this program; it will crash).
; Listing 4-4
; Uninitialized pointer demonstration.
; Note that this program will not
; run properly.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 4-4", 0
fmtStr byte "Pointer value= %p", nl, 0
.data
ptrVar qword ?
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 48
lea rcx, fmtStr
mov rdx, ptrVar
mov rdx, [rdx] ; Will crash system
call printf
add rsp, 48
ret ; Returns to caller
asmMain endp
endListing 4-4: Uninitialized pointer demonstration
Although variables you declare in the .data section are, technically, initialized, static initialization still doesn’t initialize the pointer in this program with a valid address (it initializes the pointer with 0, which is NULL).
Of course, there is no such thing as a truly uninitialized variable on the x86-64. What you really have are variables that you’ve explicitly given an initial value to and variables that just happen to inherit whatever bit pattern was in memory when storage for the variable was allocated. Much of the time, these garbage bit patterns lying around in memory don’t correspond to a valid memory address. Attempting to dereference such a pointer (that is, access the data in memory at which it points) typically raises a memory access violation exception.
Sometimes, however, those random bits in memory just happen to correspond to a valid memory location you can access. In this situation, the CPU will access the specified memory location without aborting the program. Although to a naive programmer this situation may seem preferable to stopping the program, in reality this is far worse because your defective program continues to run without alerting you to the problem. If you store data through an uninitialized pointer, you may very well overwrite the values of other important variables in memory. This defect can produce some very difficult-to-locate problems in your program.
The second problem programmers have with pointers is storing invalid address values into a pointer. The first problem is actually a special case of this second problem (with garbage bits in memory supplying the invalid address rather than you producing it via a miscalculation). The effects are the same; if you attempt to dereference a pointer containing an invalid address, you either will get a memory access violation exception or will access an unexpected memory location.
The third problem listed is also known as the dangling pointer problem. To understand this problem, consider the following code fragment:
mov rcx, 256
call malloc ; Allocate some storage
mov ptrVar, rax ; Save address away in ptrVar
.
. ; Code that uses the pointer variable ptrVar.
.
mov rcx, ptrVar
call free ; Free storage associated with ptrVar
.
. ; Code that does not change the value in ptrVar.
.
mov rbx, ptrVar
mov [rbx], alIn this example, the program allocates 256 bytes of storage and saves the address of that storage in the ptrVar variable. Then the code uses this block of 256 bytes for a while and frees the storage, returning it to the system for other uses. Note that calling free() does not change the value of ptrVar in any way; ptrVar still points at the block of memory allocated by malloc() earlier. Indeed, free() does not change any data in this block, so upon return from free(), ptrVar still points at the data stored into the block by this code.
However, note that the call to free() tells the system that the program no longer needs this 256-byte block of memory and the system can use this region of memory for other purposes. The free() function cannot enforce the fact that you will never access this data again; you are simply promising that you won’t. Of course, the preceding code fragment breaks this promise; as you can see in the last two instructions, the program fetches the value in ptrVar and accesses the data it points at in memory.
The biggest problem with dangling pointers is that you can get away with using them a good part of the time. As long as the system doesn’t reuse the storage you’ve freed, using a dangling pointer produces no ill effects in your program. However, with each new call to malloc(), the system may decide to reuse the memory released by that previous call to free(). When this happens, any attempt to dereference the dangling pointer may produce unintended consequences. The problems range from reading data that has been overwritten (by the new, legal use of the data storage), to overwriting the new data, to (the worst case) overwriting system heap management pointers (doing so will probably cause your program to crash). The solution is clear: never use a pointer value once you free the storage associated with that pointer.
Of all the problems, the fourth (failing to free allocated storage) will probably have the least impact on the proper operation of your program. The following code fragment demonstrates this problem:
mov rcx, 256
call malloc
mov ptrVar, rax
. ; Code that uses ptrVar.
. ; This code does not free up the storage
. ; associated with ptrVar.
mov rcx, 512
call malloc
mov ptrVar, rax
; At this point, there is no way to reference the original
; block of 256 bytes pointed at by ptrVar.In this example, the program allocates 256 bytes of storage and references this storage by using the ptrVar variable. At some later time, the program allocates another block of bytes and overwrites the value in ptrVar with the address of this new block. Note that the former value in ptrVar is lost. Because the program no longer has this address value, there is no way to call free() to return the storage for later use.
As a result, this memory is no longer available to your program. While making 256 bytes of memory inaccessible to your program may not seem like a big deal, imagine that this code is in a loop that repeats over and over again. With each execution of the loop, the program loses another 256 bytes of memory. After a sufficient number of loop iterations, the program will exhaust the memory available on the heap. This problem is often called a memory leak because the effect is the same as though the memory bits were leaking out of your computer (yielding less and less available storage) during program execution.
Memory leaks are far less damaging than dangling pointers. Indeed, memory leaks create only two problems: the danger of running out of heap space (which, ultimately, may cause the program to abort, though this is rare) and performance problems due to virtual memory page swapping. Nevertheless, you should get in the habit of always freeing all storage once you have finished using it. When your program quits, the operating system reclaims all storage, including the data lost via memory leaks. Therefore, memory lost via a leak is lost only to your program, not the whole system.
The last problem with pointers is the lack of type-safe access. This can occur because MASM cannot and does not enforce pointer type checking. For example, consider the program in Listing 4-5.
; Listing 4-5
; Demonstration of lack of type
; checking in assembly language
; pointer access.
option casemap:none
nl = 10
maxLen = 256
.const
ttlStr byte "Listing 4-5", 0
prompt byte "Input a string: ", 0
fmtStr byte "%d: Hex value of char read: %x", nl, 0
.data
bufPtr qword ?
bytesRead qword ?
.code
externdef readLine:proc
externdef printf:proc
externdef malloc:proc
externdef free:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbx ; Preserve RBX
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 40
; C standard library malloc function.
; Allocate sufficient characters
; to hold a line of text input
; by the user:
mov rcx, maxLen ; Allocate 256 bytes
call malloc
mov bufPtr, rax ; Save pointer to buffer
; Read a line of text from the user and place in
; the newly allocated buffer:
lea rcx, prompt ; Prompt user to input
call printf ; a line of text
mov rcx, bufPtr ; Pointer to input buffer
mov rdx, maxLen ; Maximum input buffer length
call readLine ; Read text from user
cmp rax, -1 ; Skip output if error
je allDone
mov bytesRead, rax ; Save number of chars read
; Display the data input by the user:
xor rbx, rbx ; Set index to zero
dispLp: mov r9, bufPtr ; Pointer to buffer
mov rdx, rbx ; Display index into buffer
mov r8d, [r9+rbx*1] ; Read dword rather than byte!
lea rcx, fmtStr
call printf
inc rbx ; Repeat for each char in buffer
cmp rbx, bytesRead
jb dispLp
; Free the storage by calling
; C standard library free function.
; free(bufPtr);
allDone:
mov rcx, bufPtr
call free
add rsp, 40
pop rbx ; Restore RBX
ret ; Returns to caller
asmMain endp
endListing 4-5: Type-unsafe pointer access example
Here are the commands to build and run this sample program:
C:\>build listing4-5
C:\>echo off
Assembling: listing4-5.asm
c.cpp
C:\>listing4-5
Calling Listing 4-5:
Input a string: Hello, World!
0: Hex value of char read: 6c6c6548
1: Hex value of char read: 6f6c6c65
2: Hex value of char read: 2c6f6c6c
3: Hex value of char read: 202c6f6c
4: Hex value of char read: 57202c6f
5: Hex value of char read: 6f57202c
6: Hex value of char read: 726f5720
7: Hex value of char read: 6c726f57
8: Hex value of char read: 646c726f
9: Hex value of char read: 21646c72
10: Hex value of char read: 21646c
11: Hex value of char read: 2164
12: Hex value of char read: 21
13: Hex value of char read: 5c000000
Listing 4-5 terminatedThe program in Listing 4-5 reads data from the user as character values and then displays the data as double-word hexadecimal values. While a powerful feature of assembly language is that it lets you ignore data types at will and automatically coerce the data without any effort, this power is a two-edged sword. If you make a mistake and access indirect data by using the wrong data type, MASM and the x86-64 may not catch the mistake, and your program may produce inaccurate results. Therefore, when using pointers and indirection in your programs, you need to take care that you use the data consistently with respect to data type.
This demonstration program has one fundamental flaw that could create a problem for you: when reading the last two characters of the input buffer, the program accesses data beyond the characters input by the user. If the user inputs 255 characters (plus the zero-terminating byte that readLine() appends), this program will access data beyond the end of the buffer allocated by malloc(). In theory, this could cause the program to crash. This is yet another problem that can occur when accessing data by using the wrong type via pointers.
4.7 Composite Data Types
Composite data types, also known as aggregate data types, are those that are built up from other (generally scalar) data types. The next sections cover several of the more important composite data types—character strings, arrays, multidimensional arrays, records/structs, and unions. A string is a good example of a composite data type; it is a data structure built up from a sequence of individual characters and other data.
4.8 Character Strings
After integer values, character strings are probably the most common data type that modern programs use. The x86-64 does support a handful of string instructions, but these instructions are really intended for block memory operations, not a specific implementation of a character string. Therefore, this section will provide a couple of definitions of character strings and discuss how to process them.
In general, a character string is a sequence of ASCII characters that possesses two main attributes: a length and character data. Different languages use different data structures to represent strings. Assembly language (at least, sans any library routines) doesn’t really care how you implement strings. All you need to do is create a sequence of machine instructions to process the string data in whatever format the strings take.
4.8.1 Zero-Terminated Strings
Without question, zero-terminated strings are the most common string representation in use today because this is the native string format for C, C++, and other languages. A zero-terminated string consists of a sequence of zero or more ASCII characters ending with a 0 byte. For example, in C/C++, the string "abc" requires 4 bytes: the three characters a, b, and c followed by a 0. As you’ll soon see, MASM character strings are upward compatible with zero-terminated strings, but in the meantime, you should note that creating zero-terminated strings in MASM is easy. The easiest place to do this is in the .data section by using code like the following:
.data
zeroString byte "This is the zero-terminated string", 0Whenever a character string appears in the byte directive as it does here, MASM emits each character in the string to successive memory locations. The zero value at the end of the string terminates this string.
Zero-terminated strings have two principal attributes: they are simple to implement, and the strings can be any length. On the other hand, zero-terminated strings have a few drawbacks. First, though not usually important, zero-terminated strings cannot contain the NUL character (whose ASCII code is 0). Generally, this isn’t a problem, but it does create havoc once in a while. The second problem with zero-terminated strings is that many operations on them are somewhat inefficient. For example, to compute the length of a zero-terminated string, you must scan the entire string looking for that 0 byte (counting characters up to the 0). The following program fragment demonstrates how to compute the length of the preceding string:
lea rbx, zeroString
xor rax, rax ; Set RAX to zero
whileLp: cmp byte ptr [rbx+rax*1], 0
je endwhile
inc rax
jmp whileLp
endwhile:
; String length is now in RAX.As you can see from this code, the time it takes to compute the length of the string is proportional to the length of the string; as the string gets longer, it takes longer to compute its length.
4.8.2 Length-Prefixed Strings
The length-prefixed string format overcomes some of the problems with zero-terminated strings. Length-prefixed strings are common in languages like Pascal; they generally consist of a length byte followed by zero or more character values. The first byte specifies the string length, and the following bytes (up to the specified length) are the character data. In a length-prefixed scheme, the string "abc" would consist of the 4 bytes: 03 (the string length) followed by a, b, and c. You can create length-prefixed strings in MASM by using code like the following:
.data
lengthPrefixedString label byte;
byte 3, "abc"Counting the characters ahead of time and inserting them into the byte statement, as was done here, may seem like a major pain. Fortunately, there are ways to have MASM automatically compute the string length for you.
Length-prefixed strings solve the two major problems associated with zero-terminated strings. It is possible to include the NUL character in length-prefixed strings, and those operations on zero-terminated strings that are relatively inefficient (for example, string length) are more efficient when using length-prefixed strings. However, length-prefixed strings have their own drawbacks. The principal drawback is that they are limited to a maximum of 255 characters in length (assuming a 1-byte length prefix).
Of course, if you have a problem with a string length limitation of 255 characters, it’s perfectly possible to create a length-prefixed string by using any number of bytes for the length as needed. For example, the High-Level Assembler (HLA) uses a 4-byte length variant of length-prefixed strings, allowing strings up to 4GB long.6 The point is that in assembly language, you can define string formats however you like.
If you want to create length-prefixed strings in your assembly language programs, you don’t want to have to manually count the characters in the string and emit that length in your code. It’s far better to have the assembler do this kind of grunge work for you. This is easily accomplished using the location counter operator ($) as follows:
.data
lengthPrefixedString label byte;
byte lpsLen, "abc"
lpsLen = $-lengthPrefixedString-1The lpsLen operand subtracts 1 in the address expression because $-lengthPrefixedString also includes the length prefix byte, which isn’t considered part of the string length.
4.8.3 String Descriptors
Another common string format is a string descriptor. A string descriptor is typically a small data structure (record or structure, see “Records/Structs” on page 197) that contains several pieces of data describing a string. At a bare minimum, a string descriptor will probably have a pointer to the actual string data and a field specifying the number of characters in the string (that is, the string length). Other possible fields might include the number of bytes currently occupied by the string,7 the maximum number of bytes the string could occupy, the string encoding (for example, ASCII, Latin-1, UTF-8, or UTF-16), and any other information the string data structure’s designer could dream up.
By far, the most common descriptor format incorporates a pointer to the string’s data and a size field specifying the number of bytes currently occupied by that string data. Note that this particular string descriptor is not the same thing as a length-prefixed string. In a length-prefixed string, the length immediately precedes the character data itself. In a descriptor, the length and a pointer are kept together, and this pair is (usually) separate from the character data itself.
4.8.4 Pointers to Strings
Most of the time, an assembly language program won’t directly work with strings appearing in the .data (or .const or .data?) section. Instead, the program will work with pointers to strings (including strings whose storage the program has dynamically allocated with a call to a function like malloc()). Listing 4-5 provided a simple (if not broken) example. In such applications, your assembly code will typically load a pointer to a string into a base register and then use a second (index) register to access individual characters in the string.
4.8.5 String Functions
Unfortunately, very few assemblers provide a set of string functions you can call from your assembly language programs.8 As an assembly language programmer, you’re expected to write these functions on your own. Fortunately, a couple of solutions are available if you don’t quite feel up to the task.
The first set of string functions you can call (without having to write them yourself) is the C Standard Library string functions (from the string.h header file in C). Of course, you’ll have to use C strings (zero-terminated strings) in your code when calling C Standard Library functions, but this generally isn’t a big problem. Listing 4-6 provides examples of calls to various C string functions.
; Listing 4-6
; Calling C Standard Library string functions.
option casemap:none
nl = 10
maxLen = 256
.const
ttlStr byte "Listing 4-6", 0
prompt byte "Input a string: ", 0
fmtStr1 byte "After strncpy, resultStr='%s'", nl, 0
fmtStr2 byte "After strncat, resultStr='%s'", nl, 0
fmtStr3 byte "After strcmp (3), eax=%d", nl, 0
fmtStr4 byte "After strcmp (4), eax=%d", nl, 0
fmtStr5 byte "After strcmp (5), eax=%d", nl, 0
fmtStr6 byte "After strchr, rax='%s'", nl, 0
fmtStr7 byte "After strstr, rax='%s'", nl, 0
fmtStr8 byte "resultStr length is %d", nl, 0
str1 byte "Hello, ", 0
str2 byte "World!", 0
str3 byte "Hello, World!", 0
str4 byte "hello, world!", 0
str5 byte "HELLO, WORLD!", 0
.data
strLength dword ?
resultStr byte maxLen dup (?)
.code
externdef readLine:proc
externdef printf:proc
externdef malloc:proc
externdef free:proc
; Some C standard library string functions:
; size_t strlen(char *str)
externdef strlen:proc
; char *strncat(char *dest, const char *src, size_t n)
externdef strncat:proc
; char *strchr(const char *str, int c)
externdef strchr:proc
; int strcmp(const char *str1, const char *str2)
externdef strcmp:proc
; char *strncpy(char *dest, const char *src, size_t n)
externdef strncpy:proc
; char *strstr(const char *inStr, const char *search4)
externdef strstr:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 48
; Demonstrate the strncpy function to copy a
; string from one location to another:
lea rcx, resultStr ; Destination string
lea rdx, str1 ; Source string
mov r8, maxLen ; Max number of chars to copy
call strncpy
lea rcx, fmtStr1
lea rdx, resultStr
call printf
; Demonstrate the strncat function to concatenate str2 to
; the end of resultStr:
lea rcx, resultStr
lea rdx, str2
mov r8, maxLen
call strncat
lea rcx, fmtStr2
lea rdx, resultStr
call printf
; Demonstrate the strcmp function to compare resultStr
; with str3, str4, and str5:
lea rcx, resultStr
lea rdx, str3
call strcmp
lea rcx, fmtStr3
mov rdx, rax
call printf
lea rcx, resultStr
lea rdx, str4
call strcmp
lea rcx, fmtStr4
mov rdx, rax
call printf
lea rcx, resultStr
lea rdx, str5
call strcmp
lea rcx, fmtStr5
mov rdx, rax
call printf
; Demonstrate the strchr function to search for
; "," in resultStr:
lea rcx, resultStr
mov rdx, ','
call strchr
lea rcx, fmtStr6
mov rdx, rax
call printf
; Demonstrate the strstr function to search for
; str2 in resultStr:
lea rcx, resultStr
lea rdx, str2
call strstr
lea rcx, fmtStr7
mov rdx, rax
call printf
; Demonstrate a call to the strlen function:
lea rcx, resultStr
call strlen
lea rcx, fmtStr8
mov rdx, rax
call printf
add rsp, 48
ret ; Returns to caller
asmMain endp
endListing 4-6: Calling C Standard Library string function from MASM source code
Here are the commands to build and run Listing 4-6:
C:\>build listing4-6
C:\>echo off
Assembling: listing4-6.asm
c.cpp
C:\>listing4-6
Calling Listing 4-6:
After strncpy, resultStr='Hello, '
After strncat, resultStr='Hello, World!'
After strcmp (3), eax=0
After strcmp (4), eax=-1
After strcmp (5), eax=1
After strchr, rax=', World!'
After strstr, rax='World!'
resultStr length is 13
Listing 4-6 terminatedOf course, you could make a good argument that if all your assembly code does is call a bunch of C Standard Library functions, you should have written your application in C in the first place. Most of the benefits of writing code in assembly language happen only when you “think” in assembly language, not C. In particular, you can dramatically improve the performance of your string function calls if you stop using zero-terminated strings and switch to another string format (such as length-prefixed or descriptor-based strings that include a length component).
In addition to the C Standard Library, you can find lots of x86-64 string functions written in assembly language out on the internet. A good place to start is the MASM Forum at https://masm32.com/board/ (despite the name, this message forum supports 64-bit as well as 32-bit MASM programming). Chapter 14 discusses string functions written in assembly language in greater detail.
4.9 Arrays
Along with strings, arrays are probably the most commonly used composite data. Yet most beginning programmers don’t understand how arrays operate internally and their associated efficiency trade-offs. It’s surprising how many novice (and even advanced!) programmers view arrays from a completely different perspective once they learn how to deal with arrays at the machine level.
Abstractly, an array is an aggregate data type whose members (elements) are all the same type. Selection of a member from the array is by an integer index.9 Different indices select unique elements of the array. This book assumes that the integer indices are contiguous (though this is by no means required). That is, if the number x is a valid index into the array and y is also a valid index, with x < y, then all i such that x < i < y are valid indices.
Whenever you apply the indexing operator to an array, the result is the specific array element chosen by that index. For example, A[i] chooses the ith element from array A. There is no formal requirement that element i be anywhere near element i+1 in memory. As long as A[i] always refers to the same memory location and A[i+1] always refers to its corresponding location (and the two are different), the definition of an array is satisfied.
In this book, we assume that array elements occupy contiguous locations in memory. An array with five elements will appear in memory as Figure 4-1 shows.

Figure 4-1: Array layout in memory
The base address of an array is the address of the first element in the array and always appears in the lowest memory location. The second array element directly follows the first in memory, the third element follows the second, and so on. Indices are not required to start at zero. They may start with any number as long as they are contiguous. However, for the purposes of discussion, this book will start all indexes at zero.
To access an element of an array, you need a function that translates an array index to the address of the indexed element. For a single-dimensional array, this function is very simple:
element_address = base_address + ((index - initial_index) * element_size)where initial_index is the value of the first index in the array (which you can ignore if it’s zero), and the value element_size is the size, in bytes, of an individual array element.
4.9.1 Declaring Arrays in Your MASM Programs
Before you can access elements of an array, you need to set aside storage for that array. Fortunately, array declarations build on the declarations you’ve already seen. To allocate n elements in an array, you would use a declaration like the following in one of the variable declaration sections:
array_name base_type n dup (?)array_name is the name of the array variable, and base_type is the type of an element of that array. This declaration sets aside storage for the array. To obtain the base address of the array, just use array_name.
The n dup (?) operand tells MASM to duplicate the object n times. Now let’s look at some specific examples:
.data
; Character array with elements 0 to 127.
CharArray byte 128 dup (?)
; Array of bytes with elements 0 to 9.
ByteArray byte 10 dup (?)
; Array of double words with elements 0 to 3.
DWArray dword 4 dup (?)These examples all allocate storage for uninitialized arrays. You may also specify that the elements of the arrays be initialized using declarations like the following in the .data and .const sections:
RealArray real4 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
IntegerAry sdword 1, 1, 1, 1, 1, 1, 1, 1Both definitions create arrays with eight elements. The first definition initializes each 4-byte real value to 1.0, and the second declaration initializes each 32-bit integer (sdword) element to 1.
If all the array elements have the same initial value, you can save a little work by using the following declarations:
RealArray real4 8 dup (1.0)
IntegerAry sdword 8 dup (1)These operand fields tell MASM to make eight copies of the value inside the parentheses. In past examples, this has always been ? (an uninitialized value). However, you can put an initial value inside the parentheses, and MASM will duplicate that value. In fact, you can put a comma-separated list of values, and MASM will duplicate everything inside the parentheses:
RealArray real4 4 dup (1.0, 2.0)
IntegerAry sdword 4 dup (1, 2)These two examples also create eight-element arrays. Their initial values will be 1.0, 2.0, 1.0, 2.0, 1.0, 2.0, 1.0, 2.0, and 1, 2, 1, 2, 1, 2, 1, 2, respectively.
4.9.2 Accessing Elements of a Single-Dimensional Array
To access an element of a zero-based array, you can use this formula:
element_address = base_address + index * element_sizeIf you are operating in LARGEADDRESSAWARE:NO mode, for the base_address entry you can use the name of the array (because MASM associates the address of the first element of an array with the name of that array). If you are operating in a large address mode, you’ll need to load the base address of the array into a 64-bit (base) register; for example:
lea rbx, base_addressThe element_size entry is the number of bytes for each array element. If the object is an array of bytes, the element_size field is 1 (resulting in a very simple computation). If each element of the array is a word (or other 2-byte type), then element_size is 2, and so on. To access an element of the IntegerAry array in the previous section, you’d use the following formula (the size is 4 because each element is an sdword object):
element_address = IntegerAry + (index * 4)Assuming LARGEADDRESSAWARE:NO, the x86-64 code equivalent to the statement eax = IntegerAry[index] is as follows:
mov rbx, index
mov eax, IntegerAry[rbx*4]In large address mode (LARGEADDRESSAWARE:YES), you’d have to load the address of the array into a base register; for example:
lea rdx, IntegerAry
mov rbx, index
mov eax, [rdx + rbx*4]These two instructions don’t explicitly multiply the index register (RBX) by 4 (the size of a 32-bit integer element in IntegerAry). Instead, they use the scaled-indexed address mode to perform the multiplication.
Another thing to note about this instruction sequence is that it does not explicitly compute the sum of the base address plus the index times 4. Instead, it relies on the scaled-indexed addressing mode to implicitly compute this sum. The instruction mov eax, IntegerAry[rbx*4] loads EAX from location IntegerAry + rbx*4, which is the base address plus index*4 (because RBX contains index*4). Similarly, mov eax, [rdx+rbx*4] computes this same sum as part of the addressing mode. Sure, you could have used
lea rax, IntegerAry
mov rbx, index
shl rbx, 2 ; Sneaky way to compute 4 * RBX
add rbx, rax ; Compute base address plus index * 4
mov eax, [rbx]in place of the previous sequence, but why use five instructions when two or three will do the same job? This is a good example of why you should know your addressing modes inside and out. Choosing the proper addressing mode can reduce the size of your program, thereby speeding it up.
However, if you need to multiply by a constant other than 1, 2, 4, or 8, then you cannot use the scaled-indexed addressing modes. Similarly, if you need to multiply by an element size that is not a power of 2, you will not be able to use the shl instruction to multiply the index by the element size; instead, you will have to use imul or another instruction sequence to do the multiplication.
The indexed addressing mode on the x86-64 is a natural for accessing elements of a single-dimensional array. Indeed, its syntax even suggests an array access. The important thing to keep in mind is that you must remember to multiply the index by the size of an element. Failure to do so will produce incorrect results.
The examples appearing in this section assume that the index variable is a 64-bit value. In reality, integer indexes into arrays are generally 32-bit integers or 32-bit unsigned integers. Therefore, you’d typically use the following instruction to load the index value into RBX:
mov ebx, index ; Zero-extends into RBXBecause loading a 32-bit value into a general-purpose register automatically zero-extends that register to 64 bits, the former instruction sequences (which expect a 64-bit index value) will still work properly when you’re using 32-bit integers as indexes into an array.
4.9.3 Sorting an Array of Values
Almost every textbook on this planet gives an example of a sort when introducing arrays. Because you’ve probably seen how to do a sort in high-level languages already, it’s instructive to take a quick look at a sort in MASM. Listing 4-7 uses a variant of the bubble sort, which is great for short lists of data and lists that are nearly sorted, but horrible for just about everything else.10
; Listing 4-7
; A simple bubble sort example.
; Note: This example must be assembled
; and linked with LARGEADDRESSAWARE:NO.
option casemap:none
nl = 10
maxLen = 256
true = 1
false = 0
bool typedef ptr byte
.const
ttlStr byte "Listing 4-7", 0
fmtStr byte "Sortme[%d] = %d", nl, 0
.data
; sortMe - A 16-element array to sort:
sortMe label dword
dword 1, 2, 16, 14
dword 3, 9, 4, 10
dword 5, 7, 15, 12
dword 8, 6, 11, 13
sortSize = ($ - sortMe) / sizeof dword ; Number of elements
; didSwap - A Boolean value that indicates
; whether a swap occurred on the
; last loop iteration.
didSwap bool ?
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here's the bubblesort function.
; sort(dword *array, qword count);
; Note: this is not an external (C)
; function, nor does it call any
; external functions. So it will
; dispense with some of the Windows
; calling sequence stuff.
; array - Address passed in RCX.
; count - Element count passed in RDX.
sort proc
push rax ; In pure assembly language
push rbx ; it's always a good idea
push rcx ; to preserve all registers
push rdx ; you modify
push r8
dec rdx ; numElements - 1
; Outer loop:
outer: mov didSwap, false
xor rbx, rbx ; RBX = 0
inner: cmp rbx, rdx ; while RBX < count - 1
jnb xInner
mov eax, [rcx + rbx*4] ; EAX = sortMe[RBX]
cmp eax, [rcx + rbx*4 + 4] ; If EAX > sortMe[RBX + 1]
jna dontSwap ; then swap
; sortMe[RBX] > sortMe[RBX + 1], so swap elements:
mov r8d, [rcx + rbx*4 + 4]
mov [rcx + rbx*4 + 4], eax
mov [rcx + rbx*4], r8d
mov didSwap, true
dontSwap:
inc rbx ; Next loop iteration
jmp inner
; Exited from inner loop, test for repeat
; of outer loop:
xInner: cmp didSwap, true
je outer
pop r8
pop rdx
pop rcx
pop rbx
pop rax
ret
sort endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbx
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 40
; Sort the "sortMe" array:
lea rcx, sortMe
mov rdx, sortSize ; 16 elements in array
call sort
; Display the sorted array:
xor rbx, rbx
dispLp: mov r8d, sortMe[rbx*4]
mov rdx, rbx
lea rcx, fmtStr
call printf
inc rbx
cmp rbx, sortSize
jb dispLp
add rsp, 40
pop rbx
ret ; Returns to caller
asmMain endp
endListing 4-7: A simple bubble sort example
Here are the commands to assemble and run this sample code:
C:\>sbuild listing4-7
C:\>echo off
Assembling: listing4-7.asm
c.cpp
C:\>listing4-7
Calling Listing 4-7:
Sortme[0] = 1
Sortme[1] = 2
Sortme[2] = 3
Sortme[3] = 4
Sortme[4] = 5
Sortme[5] = 6
Sortme[6] = 7
Sortme[7] = 8
Sortme[8] = 9
Sortme[9] = 10
Sortme[10] = 11
Sortme[11] = 12
Sortme[12] = 13
Sortme[13] = 14
Sortme[14] = 15
Sortme[15] = 16
Listing 4-7 terminatedThe bubble sort works by comparing adjacent elements in an array. The cmp instruction (before ; if EAX > sortMe[RBX + 1]) compares EAX (which contains sortMe[rbx*4]) against sortMe[rbx*4 + 4]. Because each element of this array is 4 bytes (dword), the index [rbx*4 + 4] references the next element beyond [rbx*4].
As is typical for a bubble sort, this algorithm terminates if the innermost loop completes without swapping any data. If the data is already presorted, the bubble sort is very efficient, making only one pass over the data. Unfortunately, if the data is not sorted (worst case, if the data is sorted in reverse order), then this algorithm is extremely inefficient. However, the bubble sort is easy to implement and understand (which is why introductory texts continue to use it in examples).
4.10 Multidimensional Arrays
The x86-64 hardware can easily handle single-dimensional arrays. Unfortunately, there is no magic addressing mode that lets you easily access elements of multidimensional arrays. That’s going to take some work and several instructions.
Before discussing how to declare or access multidimensional arrays, it would be a good idea to figure out how to implement them in memory. The first problem is to figure out how to store a multidimensional object into a one-dimensional memory space.
Consider for a moment a Pascal array of the form A:array[0..3,0..3] of char;. This array contains 16 bytes organized as four rows of four characters. Somehow, you’ve got to draw a correspondence with each of the 16 bytes in this array and 16 contiguous bytes in main memory. Figure 4-2 shows one way to do this.
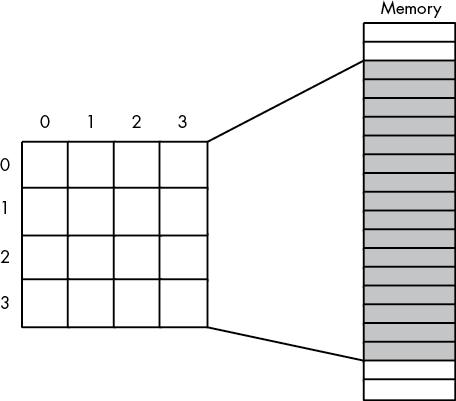
Figure 4-2: Mapping a 4×4 array to sequential memory locations
The actual mapping is not important as long as two things occur: (1) each element maps to a unique memory location (that is, no two entries in the array occupy the same memory locations) and (2) the mapping is consistent (that is, a given element in the array always maps to the same memory location). So, what you really need is a function with two input parameters (row and column) that produces an offset into a linear array of 16 memory locations.
Now any function that satisfies these constraints will work fine. Indeed, you could randomly choose a mapping as long as it was consistent. However, what you really want is a mapping that is efficient to compute at runtime and works for any size array (not just 4×4 or even limited to two dimensions). While a large number of possible functions fit this bill, two functions in particular are used by most programmers and high-level languages: row-major ordering and column-major ordering.
4.10.1 Row-Major Ordering
Row-major ordering assigns successive elements, moving across the rows and then down the columns, to successive memory locations. This mapping is demonstrated in Figure 4-3.
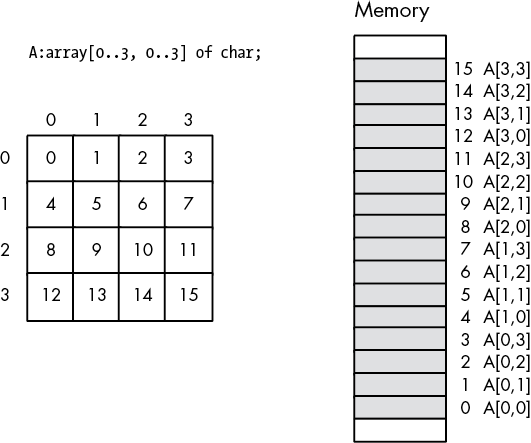
Figure 4-3: Row-major array element ordering
Row-major ordering is the method most high-level programming languages employ. It is easy to implement and use in machine language. You start with the first row (row 0) and then concatenate the second row to its end. You then concatenate the third row to the end of the list, then the fourth row, and so on (see Figure 4-4).
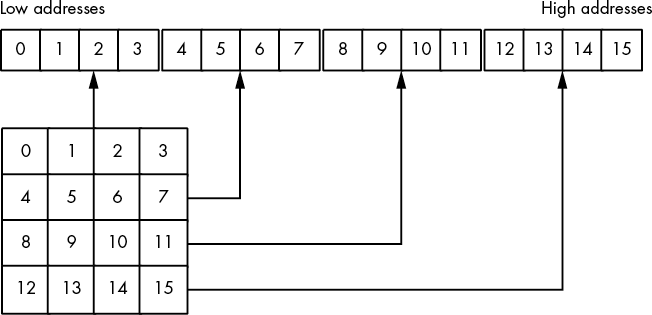
Figure 4-4: Another view of row-major ordering for a 4×4 array
The actual function that converts a list of index values into an offset is a slight modification of the formula for computing the address of an element of a single-dimensional array. The formula to compute the offset for a two-dimensional row-major ordered array is as follows:
element_address =
base_address + (col_index * row_size + row_index) * element_sizeAs usual, base_address is the address of the first element of the array (A[0][0] in this case), and element_size is the size of an individual element of the array, in bytes. col_index is the leftmost index, and row_index is the rightmost index into the array. row_size is the number of elements in one row of the array (4, in this case, because each row has four elements). Assuming element_size is 1, this formula computes the following offsets from the base address:
Column Row Offset
Index Index into Array
0 0 0
0 1 1
0 2 2
0 3 3
1 0 4
1 1 5
1 2 6
1 3 7
2 0 8
2 1 9
2 2 10
2 3 11
3 0 12
3 1 13
3 2 14
3 3 15For a three-dimensional array, the formula to compute the offset into memory is the following:
Address = Base +
((depth_index * col_size + col_index) * row_size + row_index) * element_sizeThe col_size is the number of items in a column, and row_size is the number of items in a row. In C/C++, if you’ve declared the array as type A[i][j][k];, then row_size is equal to k and col_size is equal to j.
For a four-dimensional array, declared in C/C++ as type A[i][j][k][m];, the formula for computing the address of an array element is shown here:
Address = Base +
(((left_index * depth_size + depth_index) * col_size + col_index) *
row_size + row_index) * element_sizeThe depth_size is equal to j, col_size is equal to k, and row_size is equal to m. left_index represents the value of the leftmost index.
By now you’re probably beginning to see a pattern. There is a generic formula that will compute the offset into memory for an array with any number of dimensions; however, you’ll rarely use more than four.
Another convenient way to think of row-major arrays is as arrays of arrays. Consider the following single-dimensional Pascal array definition:
A: array [0..3] of sometype;where sometype is the type sometype = array [0..3] of char;.
A is a single-dimensional array. Its individual elements happen to be arrays, but you can safely ignore that for the time being. The formula to compute the address of an element of a single-dimensional array is as follows:
element_address = Base + index * element_sizeIn this case, element_size happens to be 4 because each element of A is an array of four characters. So, this formula computes the base address of each row in this 4×4 array of characters (see Figure 4-5).
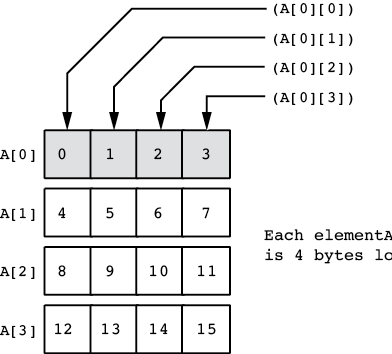
Figure 4-5: Viewing a 4×4 array as an array of arrays
Of course, once you compute the base address of a row, you can reapply the single-dimensional formula to get the address of a particular element. While this doesn’t affect the computation, it’s probably a little easier to deal with several single-dimensional computations rather than a complex multidimensional array computation.
Consider a Pascal array defined as A:array [0..3, 0..3, 0..3, 0..3, 0..3] of char;. You can view this five-dimensional array as a single-dimensional array of arrays. The following Pascal code provides such a definition:
type
OneD = array[0..3] of char;
TwoD = array[0..3] of OneD;
ThreeD = array[0..3] of TwoD;
FourD = array[0..3] of ThreeD;
var
A: array[0..3] of FourD;The size of OneD is 4 bytes. Because TwoD contains four OneD arrays, its size is 16 bytes. Likewise, ThreeD is four TwoDs, so it is 64 bytes long. Finally, FourD is four ThreeDs, so it is 256 bytes long. To compute the address of A [b, c, d, e, f], you could use the following steps:
- Compute the address of
A[b]as Base+ b *size. Here size is 256 bytes. Use this result as the new base address in the next computation. - Compute the address of
A[b, c]by the formula Base+ c *size, where Base is the value obtained in the previous step and size is 64. Use the result as the new base in the next computation. - Compute the base address of
A [b, c, d]by Base+ d *size, where Base comes from the previous computation, and size is 16. Use the result as the new base in the next computation. - Compute the address of
A[b, c, d, e]with the formula Base+ e *size, where Base comes from the previous computation, and size is 4. Use this value as the base for the next computation. - Finally, compute the address of
A[b, c, d, e, f]by using the formula Base+ f *size, where Base comes from the previous computation and size is 1 (obviously, you can ignore this final multiplication). The result you obtain at this point is the address of the desired element.
One of the main reasons you won’t find higher-dimensional arrays in assembly language is that assembly language emphasizes the inefficiencies associated with such access. It’s easy to enter something like A[b, c, d, e, f] into a Pascal program, not realizing what the compiler is doing with the code. Assembly language programmers are not so cavalier—they see the mess you wind up with when you use higher-dimensional arrays. Indeed, good assembly language programmers try to avoid two-dimensional arrays and often resort to tricks in order to access data in such an array when its use becomes absolutely mandatory.
4.10.2 Column-Major Ordering
Column-major ordering is the other function high-level languages frequently use to compute the address of an array element. FORTRAN and various dialects of BASIC (for example, older versions of Microsoft BASIC) use this method.
In row-major ordering, the rightmost index increases the fastest as you move through consecutive memory locations. In column-major ordering, the leftmost index increases the fastest. Pictorially, a column-major ordered array is organized as shown in Figure 4-6.
The formula for computing the address of an array element when using column-major ordering is similar to that for row-major ordering. You reverse the indexes and sizes in the computation.
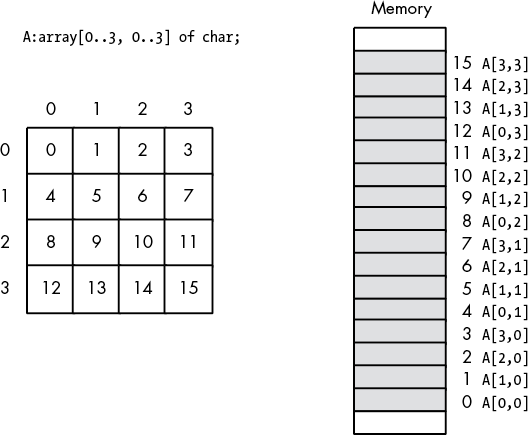
Figure 4-6: Column-major array element ordering
For a two-dimension column-major array:
element_address = base_address + (row_index * col_size + col_index) *
element_sizeFor a three-dimension column-major array:
Address = Base +
((row_index * col_size + col_index) *
depth_size + depth_index) * element_sizeFor a four-dimension column-major array:
Address =
Base + (((row_index * col_size + col_index) * depth_size + depth_index)
left_size + left_index) * element_size4.10.3 Allocating Storage for Multidimensional Arrays
If you have an m×n array, it will have m × n elements and require m × n × element_size bytes of storage. To allocate storage for an array, you must reserve this memory. As usual, there are several ways of accomplishing this task. To declare a multidimensional array in MASM, you could use a declaration like the following:
array_name element_type size1*size2*size3*...*sizen dup (?)where size1 to sizen are the sizes of each of the dimensions of the array.
For example, here is a declaration for a 4×4 array of characters:
GameGrid byte 4*4 dup (?)Here is another example that shows how to declare a three-dimensional array of strings (assuming the array holds 64-bit pointers to the strings):
NameItems qword 2 * 3 * 3 dup (?)As was the case with single-dimensional arrays, you may initialize every element of the array to a specific value by following the declaration with the values of the array constant. Array constants ignore dimension information; all that matters is that the number of elements in the array constant corresponds to the number of elements in the actual array. The following example shows the GameGrid declaration with an initializer:
GameGrid byte 'a', 'b', 'c', 'd'
byte 'e', 'f', 'g', 'h'
byte 'i', 'j', 'k', 'l'
byte 'm', 'n', 'o', 'p'This example was laid out to enhance readability (which is always a good idea). MASM does not interpret the four separate lines as representing rows of data in the array. Humans do, which is why it’s good to write the data in this manner. All that matters is that there are 16 (4 × 4) characters in the array constant. You’ll probably agree that this is much easier to read than
GameGrid byte 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j',
'k', 'l', 'm', 'n', 'o', 'p'Of course, if you have a large array, an array with really large rows, or an array with many dimensions, there is little hope for winding up with something readable. That’s when comments that carefully explain everything come in handy.
As for single-dimensional arrays, you can use the dup operator to initialize each element of a large array with the same value. The following example initializes a 256×64 array of bytes so that each byte contains the value 0FFh:
StateValue byte 256*64 dup (0FFh)The use of a constant expression to compute the number of array elements rather than simply using the constant 16,384 (256 × 64) more clearly suggests that this code is initializing each element of a 256×64 element array than does the simple literal constant 16,384.
Another MASM trick you can use to improve the readability of your programs is to use nested dup declarations. The following is an example of a MASM nested dup declaration:
StateValue byte 256 dup (64 dup (0FFh))MASM replicates anything inside the parentheses the number of times specified by the constant preceding the dup operator; this includes nested dup declarations. This example says, “Duplicate the stuff inside the parentheses 256 times.” Inside the parentheses, there is a dup operator that says, “Duplicate 0FFh 64 times,” so the outside dup operator duplicates the duplication of 64 0FFh values 256 times.
It is probably a good programming convention to declare multidimensional arrays by using the “dup of dup (. . . of dup)” syntax. This can make it clearer that you’re creating a multidimensional array rather than a single-dimensional array with a large number of elements.
4.10.4 Accessing Multidimensional Array Elements in Assembly Language
Well, you’ve seen the formulas for computing the address of a multidimensional array element. Now it’s time to see how to access elements of those arrays by using assembly language.
The mov, shl, and imul instructions make short work of the various equations that compute offsets into multidimensional arrays. Let’s consider a two-dimensional array first:
.data
i sdword ?
j sdword ?
TwoD sdword 4 dup (8 dup (?))
.
.
.
; To perform the operation TwoD[i,j] := 5;
; you'd use code like the following.
; Note that the array index computation is (i*8 + j)*4.
mov ebx, i ; Remember, zero-extends into RBX
shl rbx, 3 ; Multiply by 8
add ebx, j ; Also zero-extends result into RBX11
mov TwoD[rbx*4], 5Note that this code does not require the use of a two-register addressing mode on the x86-64 (at least, not when using the LARGEADDRESSAWARE:NO option). Although an addressing mode like TwoD[rbx][rsi] looks like it should be a natural for accessing two-dimensional arrays, that isn’t the purpose of this addressing mode.
Now consider a second example that uses a three-dimensional array (again, assuming LARGEADDRESSAWARE:NO):
.data
i dword ?
j dword ?
k dword ?
ThreeD sdword 3 dup (4 dup (5 dup (?)))
.
.
.
; To perform the operation ThreeD[i,j,k] := ESI;
; you'd use the following code that computes
; ((i*4 + j)*5 + k)*4 as the address of ThreeD[i,j,k].
mov ebx, i ; Zero-extends into RBX
shl ebx, 2 ; Four elements per column
add ebx, j
imul ebx, 5 ; Five elements per row
add ebx, k
mov ThreeD[rbx*4], esiThis code uses the imul instruction to multiply the value in RBX by 5, because the shl instruction can multiply a register by only a power of 2. While there are ways to multiply the value in a register by a constant other than a power of 2, the imul instruction is more convenient.12 Also remember that operations on the 32-bit general-purpose registers automatically zero-extend their result into the 64-bit register.
4.11 Records/Structs
Another major composite data structure is the Pascal record or C/C++/C# structure.13 The Pascal terminology is probably better, because it tends to avoid confusion with the more general term data structure. However, MASM uses the term struct, so this book favors that term.
Whereas an array is homogeneous, with elements that are all the same type, the elements in a struct can have different types. Arrays let you select a particular element via an integer index. With structs, you must select an element (known as a field) by name.
The whole purpose of a structure is to let you encapsulate different, though logically related, data into a single package. The Pascal record declaration for a student is a typical example:
student =
record
Name: string[64];
Major: integer;
SSN: string[11];
Midterm1: integer;
Midterm2: integer;
Final: integer;
Homework: integer;
Projects: integer;
end;Most Pascal compilers allocate each field in a record to contiguous memory locations. This means that Pascal will reserve the first 65 bytes for the name,14 the next 2 bytes hold the major code (assuming a 16-bit integer), the next 12 bytes hold the Social Security number, and so on.
4.11.1 MASM Struct Declarations
In MASM, you can create record types by using the struct/ends declaration. You would encode the preceding record in MASM as follows:
student struct
sName byte 65 dup (?) ; "Name" is a MASM reserved word
Major word ?
SSN byte 12 dup (?)
Midterm1 word ?
Midterm2 word ?
Final word ?
Homework word ?
Projects word ?
student endsAs you can see, the MASM declaration is similar to the Pascal declaration. To be true to the Pascal declaration, this example uses character arrays rather than strings for the sName and SSN (US Social Security number) fields. Also, the MASM declaration assumes that integers are unsigned 16-bit values (which is probably appropriate for this type of data structure).
The field names within the struct must be unique; the same name may not appear two or more times in the same record. However, all field names are local to that record. Therefore, you may reuse those field names elsewhere in the program or in different records.
The struct/ends declaration may appear anywhere in the source file as long as you define it before you use it. A struct declaration does not actually allocate any storage for a student variable. Instead, you have to explicitly declare a variable of type student. The following example demonstrates how to do this:
.data
John student {}The funny operand ({}) is a MASM-ism, just something you’ll have to remember.
The John variable declaration allocates 89 bytes of storage laid out in memory, as shown in Figure 4-7.
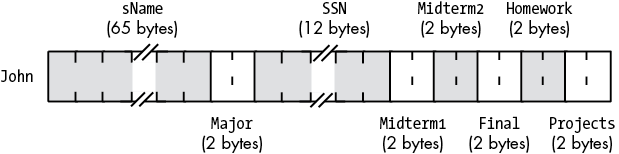
Figure 4-7: Student data structure storage in memory
If the label John corresponds to the base address of this record, the sName field is at offset John + 0, the Major field is at offset John + 65, the SSN field is at offset John + 67, and so on.
4.11.2 Accessing Record/Struct Fields
To access an element of a structure, you need to know the offset from the beginning of the structure to the desired field. For example, the Major field in the variable John is at offset 65 from the base address of John. Therefore, you could store the value in AX into this field by using this instruction:
mov word ptr John[65], axUnfortunately, memorizing all the offsets to fields in a struct defeats the whole purpose of using them in the first place. After all, if you have to deal with these numeric offsets, why not just use an array of bytes instead of a struct?
Fortunately, MASM lets you refer to field names in a record by using the same mechanism most HLLs use: the dot operator. To store AX into the Major field, you could use mov John.Major, ax instead of the previous instruction. This is much more readable and certainly easier to use.
The use of the dot operator does not introduce a new addressing mode. The instruction mov John.Major, ax still uses the PC-relative addressing mode. MASM simply adds the base address of John with the offset to the Major field (65) to get the actual displacement to encode into the instruction.
The dot operator works quite well when dealing with struct variables you declare in one of the static sections (.data, .const, or .data?) and access via the PC-relative addressing mode. However, what happens when you have a pointer to a record object? Consider the following code fragment:
mov rcx, sizeof student ; Size of student struct
call malloc ; Returns pointer in RAX
mov [rax].Final, 100Unfortunately, the Final field name is local to the student structure. As a result, MASM will complain that the name Final is undefined in this code sequence. To get around this problem, you add the structure name to the dotted name list when using pointer references. Here’s the correct form of the preceding code:
mov rcx, sizeof student ; Size of student struct
call malloc
mov [rax].student.Final, 1004.11.3 Nesting MASM Structs
MASM allows you to define fields of a structure that are themselves structure types. Consider the following two struct declarations:
grades struct
Midterm1 word ?
Midterm2 word ?
Final word ?
Homework word ?
Projects word ?
grades ends
student struct
sName byte 65 dup (?) ; "Name" is a MASM reserved word
Major word ?
SSN byte 12 dup (?)
sGrades grades {}
student endsThe sGrades field now holds all the individual grade fields that were formerly individual fields in the grades structure. Note that this particular example has the same memory layout as the previous examples (see Figure 4-7). The grades structure itself doesn’t add any new data; it simply organizes the grade fields under its own substructure.
To access the subfields, you use the same syntax you’d use with C/C++ (and most other HLLs supporting records/structures). If the John variable declaration appearing in previous sections was of this new struct type, you’d access the Homework field by using a statement such as the following:
mov ax, John.sGrades.Homework4.11.4 Initializing Struct Fields
A typical structure declaration such as the following
.data
structVar structType {}leaves all fields in structType uninitialized (similar to having the ? operand in other variable declarations). MASM will allow you to provide initial values for all the fields of a structure by supplying a list of comma-separated items between the braces in the operand field of a structure variable declaration, as shown in Listing 4-8.
; Listing 4-8
; Sample struct initialization example.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 4-8", 0
fmtStr byte "aString: maxLen:%d, len:%d, string data:'%s'"
byte nl, 0
; Define a struct for a string descriptor:
strDesc struct
maxLen dword ?
len dword ?
strPtr qword ?
strDesc ends
.data
; Here's the string data we will initialize the
; string descriptor with:
charData byte "Initial String Data", 0
len = lengthof charData ; Includes zero byte
; Create a string descriptor initialized with
; the charData string value:
aString strDesc {len, len, offset charData}
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
; "Magic" instruction offered without
; explanation at this point:
sub rsp, 48
; Display the fields of the string descriptor.
lea rcx, fmtStr
mov edx, aString.maxLen ; Zero-extends!
mov r8d, aString.len ; Zero-extends!
mov r9, aString.strPtr
call printf
add rsp, 48 ; Restore RSP
ret ; Returns to caller
asmMain endp
endListing 4-8: Initializing the fields of a structure
Here are the build commands and output for Listing 4-8:
C:\>build listing4-8
C:\>echo off
Assembling: listing4-8.asm
c.cpp
C:\>listing4-8
Calling Listing 4-8:
aString: maxLen:20, len:20, string data:'Initial String Data'
Listing 4-8 terminatedIf a structure field is an array object, you’ll need special syntax to initialize that array data. Consider the following structure definition:
aryStruct struct
aryField1 byte 8 dup (?)
aryField2 word 4 dup (?)
aryStruct endsThe initialization operands must either be a string or a single item. Therefore, the following is not legal:
a aryStruct {1,2,3,4,5,6,7,8, 1,2,3,4}This (presumably) is an attempt to initialize aryField1 with {1,2,3,4,5,6,7,8} and aryField2 with {1,2,3,4}. MASM, however, won’t accept this. MASM wants only two values in the operand field (one for aryField1 and one for aryField2). The solution is to place the array constants for the two arrays in their own set of braces:
a aryStruct {{1,2,3,4,5,6,7,8}, {1,2,3,4}}If you supply too many initializers for a given array element, MASM will report an error. If you supply too few initializers, MASM will quietly fill in the remaining array entries with 0 values:
a aryStruct {{1,2,3,4}, {1,2,3,4}}This example initializes a.aryField1 with {1,2,3,4,0,0,0,0} and initializes a.aryField2 with {1,2,3,4}.
If the field is an array of bytes, you can substitute a character string (with no more characters than the array size) for the list of byte values:
b aryStruct {"abcdefgh", {1,2,3,4}}If you supply too few characters, MASM will fill out the rest of the byte array with 0 bytes; too many characters produce an error.
4.11.5 Arrays of Structs
It is a perfectly reasonable operation to create an array of structures. To do so, you create a struct type and then use the standard array declaration syntax. The following example demonstrates how you could do this:
recElement struct
Fields for this record
recElement ends
.
.
.
.data
recArray recElement 4 dup ({})To access an element of this array, you use the standard array-indexing techniques. Because recArray is a single-dimensional array, you’d compute the address of an element of this array by using the formula base_address + index * lengthof(recElement). For example, to access an element of recArray, you’d use code like the following:
; Access element i of recArray:
; RBX := i*lengthof(recElement)
imul ebx, i, sizeOf recElement ; Zero-extends EBX to RBX!
mov eax, recArray.someField[rbx] ; LARGEADDRESSAWARE:NO!The index specification follows the entire variable name; remember, this is assembly, not a high-level language (in a high-level language, you’d probably use recArray[i].someField).
Naturally, you can create multidimensional arrays of records as well. You would use the row-major or column-major order functions to compute the address of an element within such records. The only thing that really changes (from the discussion of arrays) is that the size of each element is the size of the record object:
.data
rec2D recElement 4 dup (6 dup ({}))
.
.
.
; Access element [i,j] of rec2D and load someField into EAX:
imul ebx, i, 6
add ebx, j
imul ebx, sizeof recElement
lea rcx, rec2D ; To avoid requiring LARGEADDRESS...
mov eax, [rcx].recElement.someField[rbx*1]4.11.6 Aligning Fields Within a Record
To achieve maximum performance in your programs, or to ensure that MASM’s structures properly map to records or structures in a high-level language, you will often need to be able to control the alignment of fields within a record. For example, you might want to ensure that a double-word field’s offset is a multiple of four. You can use the align directive to do this. The following creates a structure with unaligned fields:
Padded struct
b byte ?
d dword ?
b2 byte ?
b3 byte ?
w word ?
Padded endsHere’s how MASM organizes this structure’s fields in memory:15
Name Size Offset Type
Padded . . . . . . . . . . . . . 00000009
b . . . . . . . . . . . . . . 00000000 byte
d . . . . . . . . . . . . . . 00000001 dword
b2 . . . . . . . . . . . . . . 00000005 byte
b3 . . . . . . . . . . . . . . 00000006 byte
w . . . . . . . . . . . . . . 00000007 wordAs you can see from this example, the d and w fields are both aligned on odd offsets, which may result in slower performance. Ideally, you would like d to be aligned on a double-word offset (multiple of four) and w aligned on an even offset.
You can fix this problem by adding align directives to the structure, as follows:
Padded struct
b byte ?
align 4
d dword ?
b2 byte ?
b3 byte ?
align 2
w word ?
Padded endsNow, MASM uses the following offsets for each of these fields:
Padded . . . . . . . . . . . . . 0000000C
b . . . . . . . . . . . . . . 00000000 byte
d . . . . . . . . . . . . . . 00000004 dword
b2 . . . . . . . . . . . . . . 00000008 byte
b3 . . . . . . . . . . . . . . 00000009 byte
w . . . . . . . . . . . . . . 0000000A wordAs you can see, d is now aligned on a 4-byte offset, and w is aligned at an even offset.
MASM provides one additional option that lets you automatically align objects in a struct declaration. If you supply a value (which must be 1, 2, 4, 8, or 16) as the operand to the struct statement, MASM will automatically align all fields in the structure to an offset that is a multiple of that field’s size or to the value you specify as the operand, whichever is smaller. Consider the following example:
Padded struct 4
b byte ?
d dword ?
b2 byte ?
b3 byte ?
w word ?
Padded endsHere’s the alignment MASM produces for this structure:
Padded . . . . . . . . . . . . . 0000000C
b . . . . . . . . . . . . . . 00000000 byte
d . . . . . . . . . . . . . . 00000004 dword
b2 . . . . . . . . . . . . . . 00000008 byte
b3 . . . . . . . . . . . . . . 00000009 byte
w . . . . . . . . . . . . . . 0000000A wordNote that MASM properly aligns d on a dword boundary and w on a word boundary (within the structure). Also note that w is not aligned on a dword boundary (even though the struct operand was 4). This is because MASM uses the smaller of the operand or the field’s size as the alignment value (and w’s size is 2).
4.12 Unions
A record/struct definition assigns different offsets to each field in the record according to the size of those fields. This behavior is quite similar to the allocation of memory offsets in a .data?, .data, or .const section. MASM provides a second type of structure declaration, the union, that does not assign different addresses to each object; instead, each field in a union declaration has the same offset: zero. The following example demonstrates the syntax for a union declaration:
unionType union
Fields (syntactically identical to struct declarations)
unionType endsYes, it seems rather weird that MASM still uses ends for the end of the union (rather than endu). If this really bothers you, just create a textequ for endu as follows:
endu textequ <ends>Now, you can use endu to your heart’s content to mark the end of a union.
You access the fields of a union exactly the same way you access the fields of a struct: using dot notation and field names. The following is a concrete example of a union type declaration and a variable of the union type:
numeric union
i sdword ?
u dword ?
q qword ?
numeric ends
.
.
.
.data
number numeric {}
.
.
.
mov number.u, 55
.
.
.
mov number.i, -62
.
.
.
mov rbx, number.qThe important thing to note about union objects is that all the fields of a union have the same offset in the structure. In the preceding example, the number.u, number.i, and number.q fields all have the same offset: zero. Therefore, the fields of a union overlap in memory; this is similar to the way the x86-64 8-, 16-, 32-, and 64-bit general-purpose registers overlap one another. Usually, you may access only one field of a union at a time; you do not manipulate separate fields of a particular union variable concurrently because writing to one field overwrites the other fields. In the preceding example, any modification of number.u would also change number.i and number.q.
Programmers typically use unions for two reasons: to conserve memory or to create aliases. Memory conservation is the intended use of this data structure facility. To see how this works, let’s compare the numeric union in the preceding example with a corresponding structure type:
numericRec struct
i sdword ?
u dword ?
q qword ?
numericRec endsIf you declare a variable, say n, of type numericRec, you access the fields as n.i, n.u, and n.q exactly as though you had declared the variable to be type numeric. The difference between the two is that numericRec variables allocate separate storage for each field of the structure, whereas numeric (union) objects allocate the same storage for all fields. Therefore, sizeof numericRec is 16 because the record contains two double-word fields and a quad-word (real64) field. The sizeof numeric, however, is 8. This is because all the fields of a union occupy the same memory locations, and the size of a union object is the size of the largest field of that object (see Figure 4-8).
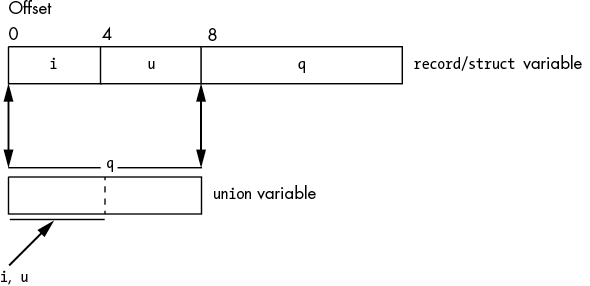
Figure 4-8: Layout of a union versus a struct variable
In addition to conserving memory, programmers often use unions to create aliases in their code. As you may recall, an alias is a different name for the same memory object. Aliases are often a source of confusion in a program, so you should use them sparingly; sometimes, however, using an alias can be quite convenient. For example, in one section of your program, you might need to constantly use type coercion to refer to an object using a different type. Although you can use a MASM textequ to simplify this process, another way to do this is to use a union variable with the fields representing the different types you want to use for the object. As an example, consider the following code:
CharOrUns union
chr byte ?
u dword ?
CharOrUns ends
.data
v CharOrUns {}With a declaration like this, you can manipulate an uns32 object by accessing v.u. If, at some point, you need to treat the LO byte of this dword variable as a character, you can do so by accessing the v.chr variable; for example:
mov v.u, eax
mov ch, v.chrYou can use unions exactly the same way you use structures in a MASM program. In particular, union declarations may appear as fields in structures, struct declarations may appear as fields in unions, array declarations may appear within unions, you can create arrays of unions, and so on.
4.12.1 Anonymous Unions
Within a struct declaration, you can place a union declaration without specifying a field name for the union object. The following example demonstrates the syntax:
HasAnonUnion struct
r real8 ?
union
u dword ?
i sdword ?
ends
s qword ?
HasAnonUnion ends
.data
v HasAnonUnion {}Whenever an anonymous union appears within a record, you can access the fields of the union as though they were unenclosed fields of the record. In the preceding example, for instance, you would access v’s u and i fields by using the syntax v.u and v.i, respectively. The u and i fields have the same offset in the record (8, because they follow a real8 object). The fields of v have the following offsets from v’s base address:
v.r 0
v.u 8
v.i 8
v.s 12sizeof(v) is 20 because the u and i fields consume only 4 bytes.
MASM also allows anonymous structures within unions. Please see the MASM documentation for more details, though the syntax and usage are identical to anonymous unions within structures.
4.12.2 Variant Types
One big use of unions in programs is to create variant types. A variant variable can change its type dynamically while the program is running. A variant object can be an integer at one point in the program, switch to a string at a different part of the program, and then change to a real value at a later time. Many very high-level language (VHLL) systems use a dynamic type system (that is, variant objects) to reduce the overall complexity of the program; indeed, proponents of many VHLLs insist that the use of a dynamic typing system is one of the reasons you can write complex programs with so few lines of code using those languages.
Of course, if you can create variant objects in a VHLL, you can certainly do it in assembly language. In this section, we’ll look at how we can use the union structure to create variant types.
At any one given instant during program execution, a variant object has a specific type, but under program control, the variable can switch to a different type. Therefore, when the program processes a variant object, it must use an if statement or switch statement (or something similar) to execute different instructions based on the object’s current type. VHLLs do this transparently.
In assembly language, you have to provide the code to test the type yourself. To achieve this, the variant type needs additional information beyond the object’s value. Specifically, the variant object needs a field that specifies the current type of the object. This field (often known as the tag field) is an enumerated type or integer that specifies the object’s type at any given instant. The following code demonstrates how to create a variant type:
VariantType struct
tag dword ? ; 0-uns32, 1-int32, 2-real64
union
u dword ?
i sdword ?
r real8 ?
ends
VariantType ends
.data
v VariantType {}The program would test the v.tag field to determine the current type of the v object. Based on this test, the program would manipulate the v.i, v.u, or v.r field.
Of course, when operating on variant objects, the program’s code must constantly be testing the tag field and executing a separate sequence of instructions for dword, sdword, or real8 values. If you use the variant fields often, it makes a lot of sense to write procedures to handle these operations for you (for example, vadd, vsub, vmul, and vdiv).
4.13 Microsoft ABI Notes
The Microsoft ABI expects fields of an array to be aligned on their natural size: the offset from the beginning of the structure to a given field must be a multiple of the field’s size. On top of this, the whole structure must be aligned at a memory address that is a multiple of the size of the largest object in the structure (up to 16 bytes). Finally, the entire structure’s size must be a multiple of the largest element in the structure (you must add padding bytes to the end of the structure to appropriately fill out the structure’s size).
The Microsoft ABI expects arrays to begin at an address in memory that is a multiple of the element size. For example, if you have an array of 32-bit objects, the array must begin on a 4-byte boundary.
Of course, if you’re not passing an array or structure data to another language (you’re only processing the struct or array in your assembly code), you can align (or misalign) the data however you want.
4.14 For More Information
For additional information about data structure representation in memory, consider reading my book Write Great Code, Volume 1 (No Starch Press, 2004). For an in-depth discussion of data types, consult a textbook on data structures and algorithms. Of course, the MASM online documentation (at https://www.microsoft.com/) is a good source of information.
4.15 Test Yourself
- What is the two-operand form of the
imulinstruction that multiplies a register by a constant? - What is the three-operand form of the
imulinstruction that multiplies a register by a constant and leaves the result in a destination register? - What is the syntax for the
imulinstruction that multiplies one register by another? - What is a manifest constant?
- Which directive(s) would you use to create a manifest constant?
- What is the difference between a text equate and a numeric equate?
- Explain how you would use an equate to define literal strings whose length is greater than eight characters.
- What is a constant expression?
- What operator would you use to determine the number of data elements in the operand field of a byte directive?
- What is the location counter?
- What operator(s) return(s) the current location counter?
- How would you compute the number of bytes between two declarations in the
.datasection? - How would you create a set of enumerated data constants using MASM?
- How do you define your own data types using MASM?
- What is a pointer (how is it implemented)?
- How do you dereference a pointer in assembly language?
- How do you declare pointer variables in assembly language?
- What operator would you use to obtain the address of a static data object (for example, in the
.datasection)? - What are the five common problems encountered when using pointers in a program?
- What is a dangling pointer?
- What is a memory leak?
- What is a composite data type?
- What is a zero-terminated string?
- What is a length-prefixed string?
- What is a descriptor-based string?
- What is an array?
- What is the base address of an array?
- Provide an example of an array declaration using the
dupoperator. - Describe how to create an array whose elements you initialize at assembly time.
- What is the formula for accessing elements of a
- Single-dimension array
dword A[10]? - Two-dimensional array
word W[4, 8]? - Three-dimensional array
real8 R[2, 4, 6]?
- Single-dimension array
- What is row-major order?
- What is column-major order?
- Provide an example of a two-dimensional array declaration (word array
W[4, 8]) using nesteddupoperators. - What is a record/struct?
- What MASM directives do you use to declare a record data structure?
- What operator do you use to access fields of a record/struct?
- What is a union?
- What directives do you use to declare unions in MASM?
- What is the difference between the memory organization of fields in a union versus those in a record/struct?
- What is an anonymous union in a struct?