8
Advanced Arithmetic

This chapter covers extended-precision arithmetic, arithmetic on operands whose sizes are different, and decimal arithmetic. By the conclusion of this chapter, you will know how to apply arithmetic and logical operations to integer operands of any size, including those larger than 64 bits, and how to convert operands of different sizes into a compatible format. Finally, you’ll learn to perform decimal arithmetic by using the x86-64 BCD instructions on the x87 FPU, which lets you use decimal arithmetic in those few applications that absolutely require base-10 operations.
8.1 Extended-Precision Operations
One big advantage of assembly language over high-level languages is that assembly language does not limit the size of integer operations. For example, the standard C programming language defines three integer sizes: short int, int, and long int.1 On the PC, these are often 16- and 32-bit integers.
Although the x86-64 machine instructions limit you to processing 8-, 16-, 32-, or 64-bit integers with a single instruction, you can use multiple instructions to process integers of any size. If you want to add 256-bit integer values together, it’s no problem. This section describes how to extend various arithmetic and logical operations from 16, 32, or 64 bits to as many bits as you please.
8.1.1 Extended-Precision Addition
The x86-64 add instruction adds two 8-, 16-, 32-, or 64-bit numbers. After the execution of add, the x86-64 carry flag is set if you have an overflow out of the HO bit of the sum. You can use this information to do extended-precision addition operations.2 Consider the way you manually perform a multiple-digit addition operation (as shown in Figure 8-1).

Figure 8-1: Multi-digit addition
The x86-64 handles extended-precision arithmetic the same way, except instead of adding the numbers a digit at a time, it adds them together a byte, word, double word, or quad word at a time. Consider the three-quad-word (192-bit) addition operation in Figure 8-2.
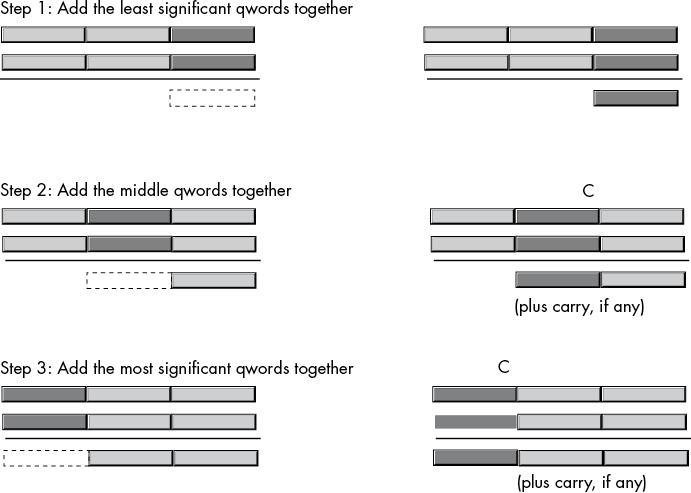
Figure 8-2: Adding two 192-bit objects together
As you can see, the idea is to break a larger operation into a sequence of smaller ones. Since the x86 processor family is capable of adding together at most 64 bits at a time (using general-purpose registers), the operation must proceed in blocks of 64 bits or fewer. Here are the steps:
- Add the two LO quad words together just as you would add the two LO digits of a decimal number together in the manual algorithm, using the
addinstruction. If there is a carry out of the LO addition,addsets the carry flag to1; otherwise, it clears the carry flag. - Add together the second pair of quad words in the two 192-bit values, plus the carry out of the previous addition (if any), using the
adc(add with carry) instruction. Theadcinstruction uses the same syntax asaddand performs almost the same operation:adc dest, source ; dest := dest + source + CThe only difference is that
adcadds in the value of the carry flag along with the source and destination operands. It sets the flags the same wayadddoes (including setting the carry flag if there is an unsigned overflow). This is exactly what we need to add together the middle two double words of our 192-bit sum. - Add the HO double words of the 192-bit value with the carry out of the sum of the middle two quad words, once again using
adc.
To summarize, the add instruction adds the LO quad words together, and adc adds all other quad word pairs together. At the end of the extended-precision addition sequence, the carry flag indicates unsigned overflow (if set), a set overflow flag indicates signed overflow, and the sign flag indicates the sign of the result. The zero flag doesn’t have any real meaning at the end of the extended-precision addition (it simply means that the sum of the two HO quad words is 0 and does not indicate that the whole result is 0).
For example, suppose that you have two 128-bit values you wish to add together, defined as follows:
.data
X oword ?
Y oword ?Suppose also that you want to store the sum in a third variable, Z, which is also an oword. The following x86-64 code will accomplish this task:
mov rax, qword ptr X ; Add together the LO 64 bits
add rax, qword ptr Y ; of the numbers and store the
mov qword ptr Z, rax ; result into the LO qword of Z
mov rax, qword ptr X[8] ; Add together (with carry) the
adc rax, qword ptr Y[8] ; HO 64 bits and store the result
mov qword ptr Z[8], rax ; into the HO qword of ZThe first three instructions add the LO quad words of X and Y together and store the result into the LO quad word of Z. The last three instructions add the HO quad words of X and Y together, along with the carry from the LO word, and store the result in the HO quad word of Z.
Remember, X, Y, and Z are oword objects (128 bits), and an instruction of the form mov rax, X would attempt to load a 128-bit value into a 64-bit register. To load a 64-bit value, specifically the LO 64 bits, the qword ptr operator coerces symbols X, Y, and Z to 64 bits. To load the HO qwords, you use address expressions of the form X[8], along with the qword ptr operator, because the x86 memory space addresses bytes, and it takes 8 consecutive bytes to form a quad word.
You can extend this algorithm to any number of bits by using adc to add in the higher-order values. For example, to add together two 256-bit values declared as arrays of four quad words, you could use code like the following:
.data
BigVal1 qword 4 dup (?)
BigVal2 qword 4 dup (?)
BigVal3 qword 4 dup (?) ; Holds the sum
.
.
.
; Note that there is no need for "qword ptr"
; because the base type of BitValx is qword.
mov rax, BigVal1[0]
add rax, BigVal2[0]
mov BigVal3[0], rax
mov rax, BigVal1[8]
adc rax, BigVal2[8]
mov BigVal3[8], rax
mov rax, BigVal1[16]
adc rax, BigVal2[16]
mov BigVal3[16], rax
mov rax, BigVal1[24]
adc rax, BigVal2[24]
mov BigVal3[24], rax8.1.2 Extended-Precision Subtraction
Just as it does addition, the x86-64 performs multi-byte subtraction the same way you would manually, except it subtracts whole bytes, words, double words, or quad words at a time rather than decimal digits. You use the sub instruction on the LO byte, word, double word, or quad word and the sbb (subtract with borrow) instruction on the high-order values.
The following example demonstrates a 128-bit subtraction using the 64-bit registers on the x86-64:
.data
Left oword ?
Right oword ?
Diff oword ?
.
.
.
mov rax, qword ptr Left
sub rax, qword ptr Right
mov qword ptr Diff, rax
mov rax, qword ptr Left[8]
sbb rax, qword ptr Right[8]
mov qword ptr Diff[8], raxThe following example demonstrates a 256-bit subtraction:
.data
BigVal1 qword 4 dup (?)
BigVal2 qword 4 dup (?)
BigVal3 qword 4 dup (?)
.
.
.
; Compute BigVal3 := BigVal1 - BigVal2.
; Note: don't need to coerce types of
; BigVa1, BigVal2, or BigVal3 because
; their base types are already qword.
mov rax, BigVal1[0]
sub rax, BigVal2[0]
mov BigVal3[0], rax
mov rax, BigVal1[8]
sbb rax, BigVal2[8]
mov BigVal3[8], rax
mov rax, BigVal1[16]
sbb rax, BigVal2[16]
mov BigVal3[16], rax
mov rax, BigVal1[24]
sbb rax, BigVal2[24]
mov BigVal3[24], rax8.1.3 Extended-Precision Comparisons
Unfortunately, there isn’t a “compare with borrow” instruction that you can use to perform extended-precision comparisons. Fortunately, you can compare extended-precision values by using just a cmp instruction, as you’ll soon see.
Consider the two unsigned values 2157h and 1293h. The LO bytes of these two values do not affect the outcome of the comparison. Simply comparing the HO bytes, 21h with 12h, tells us that the first value is greater than the second.
You need to look at both bytes of a pair of values only if the HO bytes are equal. In all other cases, comparing the HO bytes tells you everything you need to know about the values. This is true for any number of bytes, not just two. The following code compares two signed 128-bit integers by comparing their HO quad words first and comparing their LO quad words only if the HO quad words are equal:
; This sequence transfers control to location "IsGreater" if
; QwordValue > QwordValue2. It transfers control to "IsLess" if
; QwordValue < QwordValue2. It falls through to the instruction
; following this sequence if QwordValue = QwordValue2.
; To test for inequality, change the "IsGreater" and "IsLess"
; operands to "NotEqual" in this code.
mov rax, qword ptr QWordValue[8] ; Get HO qword
cmp rax, qword ptr QWordValue2[8]
jg IsGreater
jl IsLess;
mov rax, qword ptr QWordValue[0] ; If HO qwords equal,
cmp rax, qword ptr QWordValue2[0] ; then we must compare
jg IsGreater; ; the LO dwords
jl IsLess;
; Fall through to this point if the two values were equal.To compare unsigned values, use the ja and jb instructions in place of jg and jl.
You can synthesize any comparison from the preceding sequence, as shown in the following examples that demonstrate signed comparisons; just substitute ja, jae, jb, and jbe for jg, jge, jl, and jle (respectively) if you want unsigned comparisons. Each of the following examples assumes these declarations:
.data
OW1 oword ?
OW2 oword ?
OW1q textequ <qword ptr OW1>
OW2q textequ <qword ptr OW2>The following code implements a 128-bit test to see if OW1 < OW2 (signed). Control transfers to the IsLess label if OW1 < OW2. Control falls through to the next statement if this is not true:
mov rax, OW1q[8] ; Get HO dword
cmp rax, OW2q[8]
jg NotLess
jl IsLess
mov rax, OW1q[0] ; Fall through to here if the HO
cmp rax, OW2q[0] ; qwords are equal
jl IsLess
NotLess:Here is a 128-bit test to see if OW1 <= OW2 (signed). This code jumps to IsLessEq if the condition is true:
mov rax, OW1q[8] ; Get HO dword
cmp rax, OW2q[8]
jg NotLessEQ
jl IsLessEQ
mov rax, QW1q[0] ; Fall through to here if the HO
cmp rax, QW2q[0] ; qwords are equal
jle IsLessEQ
NotLessEQ:This is a 128-bit test to see if OW1 > OW2 (signed). It jumps to IsGtr if this condition is true:
mov rax, QW1q[8] ; Get HO dword
cmp rax, QW2q[8]
jg IsGtr
jl NotGtr
mov rax, QW1q[0] ; Fall through to here if the HO
cmp rax, QW2q[0] ; qwords are equal
jg IsGtr
NotGtr:The following is a 128-bit test to see if OW1 >= OW2 (signed). This code jumps to label IsGtrEQ if this is the case:
mov rax, QW1q[8] ; Get HO dword
cmp rax, QW2q[8]
jg IsGtrEQ
jl NotGtrEQ
mov rax, QW1q[0] ; Fall through to here if the HO
cmp rax, QW2q[0] ; qwords are equal
jge IsGtrEQ
NotGtrEQ:Here is a 128-bit test to see if OW1 == OW2 (signed or unsigned). This code branches to the label IsEqual if OW1 == OW2. It falls through to the next instruction if they are not equal:
mov rax, QW1q[8] ; Get HO dword
cmp rax, QW2q[8]
jne NotEqual
mov rax, QW1q[0] ; Fall through to here if the HO
cmp rax, QW2q[0] ; qwords are equal
je IsEqual
NotEqual:The following is a 128-bit test to see if OW1 != OW2 (signed or unsigned). This code branches to the label IsNotEqual if OW1 != OW2. It falls through to the next instruction if they are equal:
mov rax, QW1q[8] ; Get HO dword
cmp rax, QW2q[8]
jne IsNotEqual
mov rax, QW1q[0] ; Fall through to here if the HO
cmp rax, QW2q[0] ; qwords are equal
jne IsNotEqual
; Fall through to this point if they are equal.To generalize the preceding code for objects larger than 128 bits, start the comparison with the objects’ HO quad words and work your way down to their LO quad words, as long as the corresponding double words are equal. The following example compares two 256-bit values to see if the first is less than or equal (unsigned) to the second:
.data
Big1 qword 4 dup (?)
Big2 qword 4 dup (?)
.
.
.
mov rax, Big1[24]
cmp rax, Big2[24]
jb isLE
ja notLE
mov rax, Big1[16]
cmp rax, Big2[16]
jb isLE
ja notLE
mov rax, Big1[8]
cmp rax, Big2[8]
jb isLE
ja notLE
mov rax, Big1[0]
cmp rax, Big2[0]
jnbe notLE
isLE:
Code to execute if Big1 <= Big2
.
.
.
notLE:
Code to execute if Big1 > Big28.1.4 Extended-Precision Multiplication
Although an 8×8-, 16×16-, 32×32-, or 64×64-bit multiplication is usually sufficient, sometimes you may want to multiply larger values. You use the x86-64 single-operand mul and imul instructions for extended-precision multiplication operations, using the same techniques that you employ when manually multiplying two values. Consider the way you perform multi-digit multiplication by hand (Figure 8-3).

Figure 8-3: Multi-digit multiplication
The x86-64 does extended-precision multiplication in the same manner except that it works with bytes, words, double words, and quad words rather than digits, as shown in Figure 8-4.
Probably the most important thing to remember when performing an extended-precision multiplication is that you must also perform an extended-precision addition at the same time. Adding up all the partial products requires several additions.
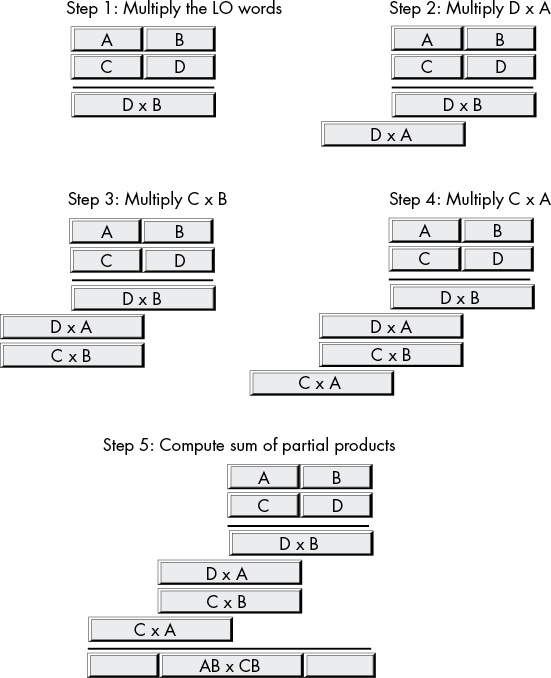
Figure 8-4: Extended-precision multiplication
Listing 8-1 demonstrates how to multiply two 64-bit values (producing a 128-bit result) by using 32-bit instructions. Technically, you can do a 64-bit multiplication with a single instruction, but this example demonstrates a method you can easily extend to 128 bits by using the x86-64 64-bit registers rather than the 32-bit registers.
; Listing 8-1
; 128-bit multiplication.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 8-1", 0
fmtStr1 byte "%d * %d = %I64d (verify:%I64d)", nl, 0
.data
op1 qword 123456789
op2 qword 234567890
product oword ?
product2 oword ?
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; mul64 - Multiplies two 64-bit values passed in RDX and RAX by
; doing a 64x64-bit multiplication, producing a 128-bit result.
; Algorithm is easily extended to 128x128 bits by switching the
; 32-bit registers for 64-bit registers.
; Stores result to location pointed at by R8.
mul64 proc
mp equ <dword ptr [rbp - 8]> ; Multiplier
mc equ <dword ptr [rbp - 16]> ; Multiplicand
prd equ <dword ptr [r8]> ; Result
push rbp
mov rbp, rsp
sub rsp, 24
push rbx ; Preserve these register values
push rcx
; Save parameters passed in registers:
mov qword ptr mp, rax
mov qword ptr mc, rdx
; Multiply the LO dword of multiplier times multiplicand.
mov eax, mp
mul mc ; Multiply LO dwords
mov prd, eax ; Save LO dword of product
mov ecx, edx ; Save HO dword of partial product result
mov eax, mp
mul mc[4] ; Multiply mp(LO) * mc(HO)
add eax, ecx ; Add to the partial product
adc edx, 0 ; Don't forget the carry!
mov ebx, eax ; Save partial product for now
mov ecx, edx
; Multiply the HO word of multiplier with multiplicand.
mov eax, mp[4] ; Get HO dword of multiplier
mul mc ; Multiply by LO word of multiplicand
add eax, ebx ; Add to the partial product
mov prd[4], eax ; Save the partial product
adc ecx, edx ; Add in the carry!
mov eax, mp[4] ; Multiply the two HO dwords together
mul mc[4]
add eax, ecx ; Add in partial product
adc edx, 0 ; Don't forget the carry!
mov prd[8], eax ; Save HO qword of result
mov prd[12], edx
; EDX:EAX contains 64-bit result at this point.
pop rcx ; Restore these registers
pop rbx
leave
ret
mul64 endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbp
mov rbp, rsp
sub rsp, 64 ; Shadow storage
; Test the mul64 function:
mov rax, op1
mov rdx, op2
lea r8, product
call mul64
; Use a 64-bit multiply to test the result:
mov rax, op1
mov rdx, op2
imul rax, rdx
mov qword ptr product2, rax
; Print the results:
lea rcx, fmtStr1
mov rdx, op1
mov r8, op2
mov r9, qword ptr product
mov rax, qword ptr product2
mov [rsp + 32], rax
call printf
leave
ret ; Returns to caller
asmMain endp
endListing 8-1: Extended-precision multiplication
The code works only for unsigned operands. To multiply two signed values, you must note the signs of the operands before the multiplication, take the absolute value of the two operands, do an unsigned multiplication, and then adjust the sign of the resulting product based on the signs of the original operands. Multiplication of signed operands is left as an exercise for you.
The example in Listing 8-1 was fairly straightforward because it was possible to keep the partial products in various registers. If you need to multiply larger values together, you will need to maintain the partial products in temporary (memory) variables. Other than that, the algorithm that Listing 8-1 uses generalizes to any number of double words.
8.1.5 Extended-Precision Division
You cannot synthesize a general n-bit / m-bit division operation by using the div and idiv instructions—though a less general operation, dividing an n-bit quantity by a 64-bit quantity can be done using the div instruction. A generic extended-precision division requires a sequence of shift and subtract instructions (which takes quite a few instructions and runs much slower). This section presents both methods (using div and shift and subtract) for extended-precision division.
8.1.5.1 Special Case Form Using div Instruction
Dividing a 128-bit quantity by a 64-bit quantity is handled directly by the div and idiv instructions, as long as the resulting quotient fits into 64 bits. However, if the quotient does not fit into 64 bits, then you have to perform extended-precision division.
For example, suppose you want to divide 0004_0000_0000_1234h by 2. The naive approach would look something like the following (assuming the value is held in a pair of qword variables named dividend, and divisor is a quad word containing 2):
; This code does *NOT* work!
mov rax, qword ptr dividend[0] ; Get dividend into EDX:EAX
mov rdx, qword ptr dividend[8]
div divisor ; Divide RDX:RAX by divisorAlthough this code is syntactically correct and will compile, it will raise a divide error exception when run. The quotient must fit into the RAX register when using div, and 2_0000_091Ah will not fit, being a 66-bit quantity (try dividing by 8 if you want to see it produce a result that will fit).
Instead, the trick is to divide the (zero- or sign-extended) HO double word of the dividend by the divisor and then repeat the process with the remainder and the LO dword of the dividend, as follows:
.data
dividend qword 1234h, 4
divisor qword 2 ; dividend/divisor = 2_0000_091Ah
quotient qword 2 dup (?)
remainder qword ?
.
.
.
mov rax, dividend[8]
xor edx, edx ; Zero-extend for unsigned division
div divisor
mov quotient[8], rax ; Save HO qword of the quotient
mov rax, dividend[0] ; This code doesn't zero-extend
div divisor ; RAX into RDX before div instr
mov quotient[0], rax ; Save LO qword of the quotient (91Ah)
mov remainder, rdx ; Save the remainderThe quotient variable is 128 bits because it’s possible for the result to require as many bits as the dividend (for example, if you divide by 1). Regardless of the size of the dividend and divisor operands, the remainder is never larger than 64 bits (in this case). Hence, the remainder variable in this example is just a quad word.
To correctly compute the 128 / 64 quotient, begin by computing the 64 / 64 quotient of dividend[8] / divisor. The quotient from this first division becomes the HO double word of the final quotient. The remainder from this division becomes the extension in RDX for the second half of the division operation. The second half of the code divides rdx:dividend[0] by divisor to produce the LO quad word of the quotient and the remainder from the division. The code does not zero-extend RAX into RDX prior to the second div instruction, because RDX already contains valid bits that must not be disturbed.
The preceding 128 / 64 division operation is a special case of the general division algorithm to divide an arbitrary-size value by a 64-bit divisor. The general algorithm is as follows:
- Move the HO quad word of the dividend into RAX and zero-extend it into RDX.
- Divide by the divisor.
- Store the value in RAX into the corresponding qword position of the quotient result variable (position of the dividend qword loaded into RAX prior to the division).
- Load RAX with the next-lower quad word in the dividend, without modifying RDX.
- Repeat steps 2 to 4 until you’ve processed all the quad words in the dividend.
At the end, the RDX register will contain the remainder, and the quotient will appear in the destination variable, where step 3 was storing the results. Listing 8-2 demonstrates how to divide a 256-bit quantity by a 64-bit divisor, producing a 256-bit quotient and a 64-bit remainder.
; Listing 8-2
; 256-bit by 64-bit division.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 8-2", 0
fmtStr1 byte "quotient = "
byte "%08x_%08x_%08x_%08x_%08x_%08x_%08x_%08x"
byte nl, 0
fmtStr2 byte "remainder = %I64x", nl, 0
.data
; op1 is a 256-bit value. Initial values were chosen
; to make it easy to verify the result.
op1 oword 2222eeeeccccaaaa8888666644440000h
oword 2222eeeeccccaaaa8888666644440000h
op2 qword 2
result oword 2 dup (0) ; Also 256 bits
remain qword 0
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; div256 - Divides a 256-bit number by a 64-bit number.
; Dividend - passed by reference in RCX.
; Divisor - passed in RDX.
; Quotient - passed by reference in R8.
; Remainder - passed by reference in R9.
div256 proc
divisor equ <qword ptr [rbp - 8]>
dividend equ <qword ptr [rcx]>
quotient equ <qword ptr [r8]>
remainder equ <qword ptr [r9]>
push rbp
mov rbp, rsp
sub rsp, 8
mov divisor, rdx
mov rax, dividend[24] ; Begin div with HO qword
xor rdx, rdx ; Zero-extend into RDS
div divisor ; Divide HO word
mov quotient[24], rax ; Save HO result
mov rax, dividend[16] ; Get dividend qword #2
div divisor ; Continue with division
mov quotient[16], rax ; Store away qword #2
mov rax, dividend[8] ; Get dividend qword #1
div divisor ; Continue with division
mov quotient[8], rax ; Store away qword #1
mov rax, dividend[0] ; Get LO dividend qword
div divisor ; Continue with division
mov quotient[0], rax ; Store away LO qword
mov remainder, rdx ; Save remainder
leave
ret
div256 endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbp
mov rbp, rsp
sub rsp, 80 ; Shadow storage
; Test the div256 function:
lea rcx, op1
mov rdx, op2
lea r8, result
lea r9, remain
call div256
; Print the results:
lea rcx, fmtStr1
mov edx, dword ptr result[28]
mov r8d, dword ptr result[24]
mov r9d, dword ptr result[20]
mov eax, dword ptr result[16]
mov [rsp + 32], rax
mov eax, dword ptr result[12]
mov [rsp + 40], rax
mov eax, dword ptr result[8]
mov [rsp + 48], rax
mov eax, dword ptr result[4]
mov [rsp + 56], rax
mov eax, dword ptr result[0]
mov [rsp + 64], rax
call printf
lea rcx, fmtStr2
mov rdx, remain
call printf
leave
ret ; Returns to caller
asmMain endp
endListing 8-2: Unsigned 128 / 32-bit extended-precision division
Here’s the build command and program output (note that you can verify that the division was correct by simply looking at the result, noting that each digit is one-half the original value):
C:\>build listing8-2
C:\>echo off
Assembling: listing8-2.asm
c.cpp
C:\>listing8-2
Calling Listing 8-2:
quotient = 11117777_66665555_44443333_22220000_11117777_66665555_44443333_22220000
remainder = 0
Listing 8-2 terminatedYou can extend this code to any number of bits by adding additional mov-div-mov instructions to the sequence. Like the extended-precision multiplication in the previous section, this extended-precision division algorithm works only for unsigned operands. To divide two signed quantities, you must note their signs, take their absolute values, do the unsigned division, and then set the sign of the result based on the signs of the operands.
8.1.5.2 Generic N-bit by M-bit Division
To use a divisor larger than 64 bits, you have to implement the division by using a shift-and-subtract strategy, which works but is very slow. As with multiplication, the best way to understand how the computer performs division is to study how you were taught to do long division by hand. Consider the operation 3456 / 12 and the steps you would take to manually perform this operation, as shown in Figure 8-5.

Figure 8-5: Manual digit-by-digit division operation
This algorithm is actually easier in binary because at each step you do not have to guess how many times 12 goes into the remainder, nor do you have to multiply 12 by your guess to obtain the amount to subtract. At each step in the binary algorithm, the divisor goes into the remainder exactly 0 or 1 time. As an example, consider the division of 27 (11011) by 3 (11) that is shown in Figure 8-6.

Figure 8-6: Longhand division in binary
The following algorithm implements this binary division operation in a way that computes the quotient and the remainder at the same time:
Quotient := Dividend;
Remainder := 0;
for i := 1 to NumberBits do
Remainder:Quotient := Remainder:Quotient SHL 1;
if Remainder >= Divisor then
Remainder := Remainder - Divisor;
Quotient := Quotient + 1;
endif
endforNumberBits is the number of bits in the Remainder, Quotient, Divisor, and Dividend variables. SHL is the left-shift operator. The Quotient := Quotient + 1; statement sets the LO bit of Quotient to 1 because this algorithm previously shifts Quotient 1 bit to the left. Listing 8-3 implements this algorithm.
; Listing 8-3
; 128-bit by 128-bit division.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 8-3", 0
fmtStr1 byte "quotient = "
byte "%08x_%08x_%08x_%08x"
byte nl, 0
fmtStr2 byte "remainder = "
byte "%08x_%08x_%08x_%08x"
byte nl, 0
fmtStr3 byte "quotient (2) = "
byte "%08x_%08x_%08x_%08x"
byte nl, 0
.data
; op1 is a 128-bit value. Initial values were chosen
; to make it easy to verify the result.
op1 oword 2222eeeeccccaaaa8888666644440000h
op2 oword 2
op3 oword 11117777666655554444333322220000h
result oword ?
remain oword ?
.code
externdef printf:proc
; Return program title to C++ program:
public getTitle
getTitle proc
lea rax, ttlStr
ret
getTitle endp
; div128 - This procedure does a general 128 / 128 division operation
; using the following algorithm (all variables are assumed
; to be 128-bit objects).
; Quotient := Dividend;
; Remainder := 0;
; for i := 1 to NumberBits do
; Remainder:Quotient := Remainder:Quotient SHL 1;
; if Remainder >= Divisor then
; Remainder := Remainder - Divisor;
; Quotient := Quotient + 1;
; endif
; endfor
; Data passed:
; 128-bit dividend, by reference in RCX.
; 128-bit divisor, by reference in RDX.
; Data returned:
; Pointer to 128-bit quotient in R8.
; Pointer to 128-bit remainder in R9.
div128 proc
remainder equ <[rbp - 16]>
dividend equ <[rbp - 32]>
quotient equ <[rbp - 32]> ; Aliased to dividend
divisor equ <[rbp - 48]>
push rbp
mov rbp, rsp
sub rsp, 48
push rax
push rcx
xor rax, rax ; Initialize remainder to 0
mov remainder, rax
mov remainder[8], rax
; Copy the dividend to local storage:
mov rax, [rcx]
mov dividend, rax
mov rax, [rcx+8]
mov dividend[8], rax
; Copy the divisor to local storage:
mov rax, [rdx]
mov divisor, rax
mov rax, [rdx + 8]
mov divisor[8], rax
mov cl, 128 ; Count off bits in CL
; Compute Remainder:Quotient := Remainder:Quotient SHL 1:
repeatLp: shl qword ptr dividend[0], 1 ; 256-bit extended-
rcl qword ptr dividend[8], 1 ; precision shift
rcl qword ptr remainder[0], 1 ; through remainder
rcl qword ptr remainder[8], 1
; Do a 128-bit comparison to see if the remainder
; is greater than or equal to the divisor.
mov rax, remainder[8]
cmp rax, divisor[8]
ja isGE
jb notGE
mov rax, remainder
cmp rax, divisor
ja isGE
jb notGE
; Remainder := Remainder - Divisor;
isGE: mov rax, divisor
sub remainder, rax
mov rax, divisor[8]
sbb remainder[8], rax
; Quotient := Quotient + 1;
add qword ptr quotient, 1
adc qword ptr quotient[8], 0
notGE: dec cl
jnz repeatLp
; Okay, copy the quotient (left in the dividend variable)
; and the remainder to their return locations.
mov rax, quotient[0]
mov [r8], rax
mov rax, quotient[8]
mov [r8][8], rax
mov rax, remainder[0]
mov [r9], rax
mov rax, remainder[8]
mov [r9][8], rax
pop rcx
pop rax
leave
ret
div128 endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbp
mov rbp, rsp
sub rsp, 64 ; Shadow storage
; Test the div128 function:
lea rcx, op1
lea rdx, op2
lea r8, result
lea r9, remain
call div128
; Print the results:
lea rcx, fmtStr1
mov edx, dword ptr result[12]
mov r8d, dword ptr result[8]
mov r9d, dword ptr result[4]
mov eax, dword ptr result[0]
mov [rsp + 32], rax
call printf
lea rcx, fmtStr2
mov edx, dword ptr remain[12]
mov r8d, dword ptr remain[8]
mov r9d, dword ptr remain[4]
mov eax, dword ptr remain[0]
mov [rsp + 32], rax
call printf
; Test the div128 function:
lea rcx, op1
lea rdx, op3
lea r8, result
lea r9, remain
call div128
; Print the results:
lea rcx, fmtStr3
mov edx, dword ptr result[12]
mov r8d, dword ptr result[8]
mov r9d, dword ptr result[4]
mov eax, dword ptr result[0]
mov [rsp + 32], rax
call printf
lea rcx, fmtStr2
mov edx, dword ptr remain[12]
mov r8d, dword ptr remain[8]
mov r9d, dword ptr remain[4]
mov eax, dword ptr remain[0]
mov [rsp + 32], rax
call printf
leave
ret ; Returns to caller
asmMain endp
endListing 8-3: Extended-precision division
Here’s the build command and program output:
C:\>build listing8-3
C:\>echo off
Assembling: listing8-3.asm
c.cpp
C:\>listing8-3
Calling Listing 8-3:
quotient = 11117777_66665555_44443333_22220000
remainder = 00000000_00000000_00000000_00000000
quotient (2) = 00000000_00000000_00000000_00000002
remainder = 00000000_00000000_00000000_00000000
Listing 8-3 terminatedThis code does not check for division by 0 (it will produce the value 0FFFF_FFFF_FFFF_FFFFh if you attempt to divide by 0); it handles only unsigned values and is very slow (an order of magnitude or two worse than the div and idiv instructions). To handle division by 0, check the divisor against 0 prior to running this code and return an appropriate error code if the divisor is 0. Dealing with signed values is the same as the earlier division algorithm: note the signs, take the operands’ absolute values, do the unsigned division, and then fix the sign afterward.
You can use the following technique to boost the performance of this division by a fair amount. Check to see if the divisor variable uses only 32 bits. Often, even though the divisor is a 128-bit variable, the value itself fits into 32 bits (that is, the HO double words of Divisor are 0) and you can use the div instruction, which is much faster. The improved algorithm is a bit more complex because you have to first compare the HO quad words for 0, but on average, it runs much faster while remaining capable of dividing any two pairs of values.
8.1.6 Extended-Precision Negation Operations
The neg instruction doesn’t provide a generic extended-precision form. However, a negation is equivalent to subtracting a value from 0, so we can easily simulate an extended-precision negation by using the sub and sbb instructions. The following code provides a simple way to negate a (320-bit) value by subtracting that value from 0, using an extended-precision subtraction:
.data
Value qword 5 dup (?) ; 320-bit value
.
.
.
xor rax, rax ; RAX = 0
sub rax, Value
mov Value, rax
mov eax, 0 ; Cannot use XOR here:
sbb rax , Value[8] ; must preserve carry!
mov Value[8], rax
mov eax, 0 ; Zero-extends!
sbb rax, Value[16]
mov Value[16], rax
mov eax, 0
sbb rax, Value[24]
mov Value[24], rax
mov rax, 0
sbb rax, Value[32]
mov Value[32], raxA slightly more efficient way to negate smaller values (128 bits) uses a combination of neg and sbb instructions. This technique uses the fact that neg subtracts its operand from 0. In particular, it sets the flags the same way the sub instruction would if you subtracted the destination value from 0. This code takes the following form (assuming you want to negate the 128-bit value in RDX:RAX):
neg rdx
neg rax
sbb rdx, 0The first two instructions negate the HO and LO qwords of the 128-bit result. However, if there is a borrow out of the LO negation (think of neg rax as subtracting 0 from RAX, possibly producing a carry/borrow), that borrow is not subtracted from the HO qword. The sbb instruction at the end of this sequence subtracts nothing from RDX if no borrow occurs when negating RAX; it subtracts 1 from RDX if a borrow was needed when subtracting 0 from RAX.
With a lot of work, it is possible to extend this scheme to more than 128 bits. However, around 256 bits (and certainly, once you get beyond 256 bits), it actually takes fewer instructions to use the general subtract-from-zero scheme.
8.1.7 Extended-Precision AND Operations
Performing an n-byte AND operation is easy: simply AND the corresponding bytes between the two operands, saving the result. For example, to perform the AND operation with all operands 128 bits long, you could use the following code:
mov rax, qword ptr source1
and rax, qword ptr source2
mov qword ptr dest, rax
mov rax, qword ptr source1[8]
and rax, qword ptr source2[8]
mov qword ptr dest[8], raxTo extend this technique to any number of qwords, logically AND the corresponding bytes, words, double words, or quad words together in the operands.
This sequence sets the flags according to the value of the last and operation. If you AND the HO quad words last, this sets all but the zero flag correctly. If you need to test the zero flag after this sequence, logically OR the two resulting double words together (or otherwise compare them both against 0).
8.1.8 Extended-Precision OR Operations
Multi-byte logical OR operations are performed in the same way as multi-byte AND operations. You OR the corresponding bytes in the two operands together. For example, to logically OR two 192-bit values, use the following code:
mov rax, qword ptr source1
or rax, qword ptr source2
mov qword ptr dest, rax
mov rax, qword ptr source1[8]
or rax, qword ptr source2[8]
mov qword ptr dest[8], rax
mov rax, qword ptr source1[16]
or rax, qword ptr source2[16]
mov qword ptr dest[16], raxAs in the previous example, this does not set the zero flag properly for the entire operation. If you need to test the zero flag after an extended-precision OR, you must logically OR all the resulting double words together.
8.1.9 Extended-Precision XOR Operations
As with other logical operations, extended-precision XOR operations exclusive-ORs the corresponding bytes in the two operands to obtain the extended-precision result. The following code sequence operates on two 64-bit operands, computes their exclusive-or, and stores the result into a 64-bit variable:
mov rax, qword ptr source1
xor rax, qword ptr source2
mov qword ptr dest, rax
mov rax, qword ptr source1[8]
xor rax, qword ptr source2[8]
mov qword ptr dest[8], raxThe comment about the zero flag in the previous two sections, as well as the comment about the XMM and YMM registers, apply here.
8.1.10 Extended-Precision NOT Operations
The not instruction inverts all the bits in the specified operand. An extended-precision NOT is performed by executing the not instruction on all the affected operands. For example, to perform a 128-bit NOT operation on the value in RDX:RAX, execute the following instructions:
not rax
not rdxKeep in mind that if you execute the NOT instruction twice, you wind up with the original value. Also, exclusive-ORing a value with all 1s (0FFh, 0FFFFh, 0FFFF_FFFFh, or 0FFFF_FFFF_FFFF_FFFFh) performs the same operation as the not instruction.
8.1.11 Extended-Precision Shift Operations
Extended-precision shift operations require a shift and a rotate instruction. This section describes how to construct these operations.
8.1.11.1 Extended-Precision Shift Left
A 128-bit shl (shift left) takes the form shown in Figure 8-7.
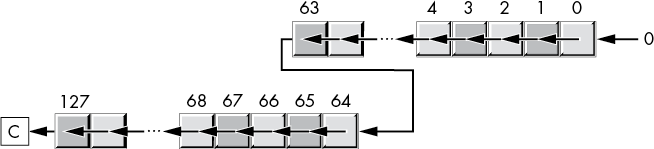
Figure 8-7: 128-bit shift-left operation
To accomplish this with machine instructions, we must first shift the LO qword to the left (for example, using the shl instruction) and capture the output from bit 63 (conveniently, the carry flag does this for us). We must then shift this bit into the LO bit of the HO qword while simultaneously shifting all the other bits to the left (and capturing the output by using the carry flag).
You can use the shl and rcl instructions to implement this 128-bit shift. For example, to shift the 128-bit quantity in RDX:RAX one position to the left, you’d use the following instructions:
shl rax, 1
rcl rdx, 1The shl instruction shifts a 0 into bit 0 of the 128-bit operand and shifts bit 63 into the carry flag. The rcl instruction then shifts the carry flag into bit 64 and shifts bit 127 into the carry flag. The result is exactly what we want.
Using this technique, you can shift an extended-precision value only 1 bit at a time. You cannot shift an extended-precision operand several bits by using the CL register, nor can you specify a constant value greater than 1 when using this technique.
To perform a shift left on an operand larger than 128 bits, use additional rcl instructions. An extended-precision shift-left operation always starts with the least-significant quad word, and each succeeding rcl instruction operates on the next-most-significant double word. For example, to perform a 192-bit shift-left operation on a memory location, you could use the following instructions:
shl qword ptr Operand[0], 1
rcl qword ptr Operand[8], 1
rcl qword ptr Operand[16], 1If you need to shift your data by 2 or more bits, you can either repeat the preceding sequence the desired number of times (for a constant number of shifts) or place the instructions in a loop to repeat them a certain number of times. For example, the following code shifts the 192-bit value Operand to the left by the number of bits specified in CL:
ShiftLoop:
shl qword ptr Operand[0], 1
rcl qword ptr Operand[8], 1
rcl qword ptr Operand[16], 1
dec cl
jnz ShiftLoop8.1.11.2 Extended-Precision Shift Right and Shift Arithmetic Right
You implement shr (shift right) and sar (shift arithmetic right) in a similar way, except you must start at the HO word of the operand and work your way down to the LO word:
; Extended-precision SAR:
sar qword ptr Operand[16], 1
rcr qword ptr Operand[8], 1
rcr qword ptr Operand[0], 1
; Extended-precision SHR:
shr qword ptr Operand[16], 1
rcr qword ptr Operand[8], 1
rcr qword ptr Operand[0], 1The extended-precision shifts set the flags differently than their 8-, 16-, 32-, and 64-bit counterparts, because the rotate instructions affect the flags differently than the shift instructions. Fortunately, the carry flag is the one you’ll test most often after a shift operation, and the extended-precision shift operations (that is, rotate instructions) properly set this flag.
8.1.11.3 Efficient Multi-bit Extended-Precision Shifts
The shld and shrd instructions let you efficiently implement extended-precision shifts of several bits. These instructions have the following syntax:
shld Operand1, Operand2, constant
shld Operand1, Operand2, cl
shrd Operand1, Operand2, constant
shrd Operand1, Operand2, clThe shld instruction works as shown in Figure 8-8.
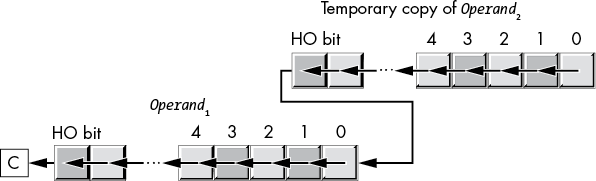
Figure 8-8: shld operation
Operand2 must be a 16-, 32-, or 64-bit register. Operand1 can be a register or a memory location. Both operands must be the same size. The third operand, constant or cl, specifies the number of bits to shift, and may be a value in the range 0 through n – 1, where n is the size of the first two operands.
The shld instruction shifts a copy of the bits in Operand2 to the left by the number of bits specified by the third operand, storing the result into the location specified by the first operand. The HO bits shift into the carry flag, and the HO bits of Operand2 shift into the LO bits of Operand1. The third operand specifies the number of bits to shift. If the count is n, then shld shifts bit n – 1 into the carry flag (obviously, this instruction maintains only the last bit shifted into the carry). The shld instruction sets the flag bits as follows:
- If the shift count is 0,
shlddoesn’t affect any flags. - The carry flag contains the last bit shifted out of the HO bit of Operand1.
- If the shift count is 1, the overflow flag will contain 1 if the sign bit of Operand1 changes during the shift. If the count is not 1, the overflow flag is undefined.
- The zero flag will be 1 if the shift produces a 0 result.
- The sign flag will contain the HO bit of the result.
The shrd instruction is similar to shld except, of course, it shifts its bits right rather than left. To get a clear picture of the shrd instruction, consider Figure 8-9.
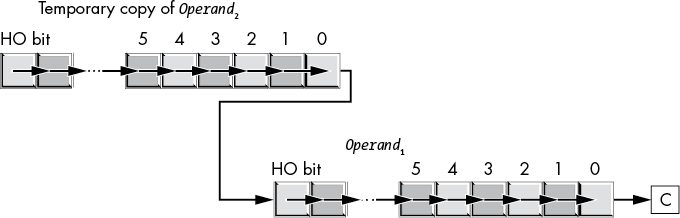
Figure 8-9: shrd operation
The shrd instruction sets the flag bits as follows:
- If the shift count is 0,
shrddoesn’t affect any flags. - The carry flag contains the last bit shifted out of the LO bit of Operand1.
- If the shift count is 1, the overflow flag will contain 1 if the HO bit of Operand1 changes. If the count is not 1, the overflow flag is undefined.
- The zero flag will be 1 if the shift produces a 0 result.
- The sign flag will contain the HO bit of the result.
Consider the following code sequence:
.data
ShiftMe qword 012345678h, 90123456h, 78901234h
.
.
.
mov rax, ShiftMe[8]
shld ShiftMe[16], rax, 6
mov rax, ShiftMe[0]
shld ShiftMe[8], rax, 6
shl ShiftMe[0], 6The first shld instruction shifts the bits from ShiftMe[8] into ShiftMe[16] without affecting the value in ShiftMe[8]. The second shld instruction shifts the bits from ShiftMe into ShiftMe[8]. Finally, the shl instruction shifts the LO double word the appropriate amount.
There are two important things to note about this code. First, unlike the other extended-precision shift-left operations, this sequence works from the HO quad word down to the LO quad word. Second, the carry flag does not contain the carry from the HO shift operation. If you need to preserve the carry flag at that point, you will need to push the flags after the first shld instruction and pop the flags after the shl instruction.
You can do an extended-precision shift-right operation by using the shrd instruction. It works almost the same way as the preceding code sequence, except you work from the LO quad word to the HO quad word. The solution is left as an exercise for you.
8.1.12 Extended-Precision Rotate Operations
The rcl and rcr operations extend in a manner similar to shl and shr. For example, to perform 192-bit rcl and rcr operations, use the following instructions:
rcl qword ptr Operand[0], 1
rcl qword ptr Operand[8], 1
rcl qword ptr Operand[16], 1
rcr qword ptr Operand[16], 1
rcr qword ptr Operand[8], 1
rcr qword ptr Operand[0], 1The only difference between this code and the code for the extended-precision shift operations is that the first instruction is a rcl or rcr rather than a shl or shr.
Performing an extended-precision rol or ror operation isn’t quite as simple because of the way the incoming bit is processed. You can use the bt, shld, and shrd instructions to implement an extended-precision rol or ror instruction.3 The following code shows how to use the shld and bt instructions to do a 128-bit extended-precision rol:
; Compute rol RDX:RAX, 4:
mov rbx, rdx
shld rdx, rax, 4
shld rax, rbx, 4
bt rbx, 28 ; Set carry flag, if desiredAn extended-precision ror instruction is similar; just keep in mind that you work on the LO end of the object first, and the HO end last.
8.2 Operating on Different-Size Operands
Occasionally, you may need to do a computation on a pair of operands that are not the same size. For example, you may need to add a word and a double word together or subtract a byte value from a word value. To do so, extend the smaller operand to the size of the larger operand and then operate on two same-size operands. For signed operands, you sign-extend the smaller operand to the same size as the larger operand; for unsigned values, you zero-extend the smaller operand. This works for any operation.
The following examples demonstrate adding a byte variable and a word variable:
.data
var1 byte ?
var2 word ?
.
.
.
; Unsigned addition:
movzx ax, var1
add ax, var2
; Signed addition:
movsx ax, var1
add ax, var2In both cases, the byte variable was loaded into the AL register, extended to 16 bits, and then added to the word operand. This code works out really well if you can choose the order of the operations (for example, adding the 8-bit value to the 16-bit value).
Sometimes you cannot specify the order of the operations. Perhaps the 16-bit value is already in the AX register, and you want to add an 8-bit value to it. For unsigned addition, you could use the following code:
mov ax, var2 ; Load 16-bit value into AX
. ; Do some other operations, leaving
. ; a 16-bit quantity in AX
add al, var1 ; Add in the 8-bit value
adc ah, 0 ; Add carry into the HO wordThe first add instruction adds the byte at var1 to the LO byte of the value in the accumulator. The adc instruction adds the carry from the addition of the LO bytes into the HO byte of the accumulator. If you leave out adc, you may not get the correct result.
Adding an 8-bit signed operand to a 16-bit signed value is a little more difficult. Unfortunately, you cannot add an immediate value (as in the preceding example) to the HO word of AX, because the HO extension byte can be either 0 or 0FFh. If a register is available, the best thing to do is the following:
mov bx, ax ; BX is the available register
movsx ax, var1
add ax, bxIf an extra register is not available, you might try the following code:
push ax ; Save word value
movsx ax, var1 ; Sign-extend 8-bit operand to 16 bits
add ax, [rsp] ; Add in previous word value
add rsp, 2 ; Pop junk from stackThis works because the x86-64 can push 16-bit registers. One word of advice: don’t leave the RSP register misaligned (not on an 8-byte boundary) for very long. If you’re working with 32- or 64-bit registers, you’ll have to push the full 64-bit register and add 8 to RSP when you’re done with the stack.
Another alternative is to store the 16-bit value in the accumulator into a memory location and then proceed as before:
mov temp, ax
movsx ax, var1
add ax, tempAll these examples add a byte value to a word value. By zero- or sign-extending the smaller operand to the size of the larger operand, you can easily add any two different-size variables together.
As a last example, consider adding an 8-bit signed value to an oword (128-bit) value:
.data
OVal qword ?
BVal byte ?
.
.
.
movsx rax, BVal
cqo
add rax, qword ptr OVal
adc rdx, qword ptr OVal[8]8.3 Decimal Arithmetic
The x86-64 CPUs use the binary numbering system for their native internal representation. In the early days of computing, designers thought that decimal (base-10) arithmetic was more accurate for business calculations. Mathematicians have shown that this is not the case; nevertheless, some algorithms depend on decimal calculations to produce correct results. Therefore, although decimal arithmetic is generally less efficient and less accurate than using binary arithmetic, the need for decimal arithmetic persists.
To represent decimal numbers in the native binary format, the most common technique is to use the binary-coded decimal (BCD) representation. This uses 4 bits to represent the 10 possible decimal digits (see Table 8-1). The binary value of those 4 bits is equal to the corresponding decimal value in the range 0 to 9. Of course, with 4 bits we can actually represent 16 different values; the BCD format ignores the remaining six bit combinations. Because each BCD digit requires 4 bits, we can represent a two-digit BCD value with a single byte. This means that we can represent the decimal values in the range 0 to 99 by using a single byte (as opposed to 0 to 255 with a byte in binary format).
Table 8-1: Binary-Coded Decimal Representation
| BCD representation | Decimal equivalent |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | Illegal |
| 1011 | Illegal |
| 1100 | Illegal |
| 1101 | Illegal |
| 1110 | Illegal |
| 1111 | Illegal |
8.3.1 Literal BCD Constants
MASM does not provide, nor do you need, a literal BCD constant. Because BCD is just a form of hexadecimal notation that does not allow the values 0Ah to 0Fh, you can easily create BCD constants by using MASM’s hexadecimal notation. For example, the following mov instruction copies the BCD value 99 into the AL register:
mov al, 99hThe important thing to keep in mind is that you must not use MASM literal decimal constants for BCD values. That is, mov al, 95 does not load the BCD representation for 95 into the AL register. Instead, it loads 5Fh into AL, and that’s an illegal BCD value.
8.3.2 Packed Decimal Arithmetic Using the FPU
To improve the performance of applications that rely on decimal arithmetic, Intel incorporated support for decimal arithmetic directly into the FPU. The FPU supports values with up to 18 decimal digits of precision, with computations using all the arithmetic capabilities of the FPU, from addition to transcendental operations. Assuming you can live with only 18 digits of precision and a few other restrictions, decimal arithmetic on the FPU is the right way to go.
The FPU supports only one BCD data type: a 10-byte 18-digit packed decimal value. The packed decimal format uses the first 9 bytes to hold the BCD value in a standard packed decimal format. The first byte contains the two LO digits, and the ninth byte holds the two HO digits. The HO bit of the tenth byte holds the sign bit, and the FPU ignores the remaining bits in the tenth byte (as using those bits would create possible BCD values that the FPU could not exactly represent in the native floating-point format).
The FPU uses a one’s complement notation for negative BCD values. The sign bit contains a 1 if the number is negative, and it contains a 0 if the number is positive. If the number is 0, the sign bit may be either 0 or 1, because, like the binary one’s complement format, there are two distinct representations for 0.
MASM’s tbyte type is the standard data type used to define packed BCD variables. The fbld and fbstp instructions require a tbyte operand (which you can initialize with a hexadecimal/BCD value).
Instead of fully supporting decimal arithmetic, the FPU provides two instructions, fbld and fbstp, that convert between packed decimal and binary floating-point formats when moving data to and from the FPU. The fbld (float/BCD load) instruction loads an 80-bit packed BCD value onto the top of the FPU stack after converting that BCD value to the binary floating-point format. Likewise, the fbstp (float/BCD store and pop) instruction pops the floating-point value off the top of stack, converts it to a packed BCD value, and stores the BCD value into the destination memory location. This means calculations are done using binary arithmetic. If you have an algorithm that absolutely, positively depends on the use of decimal arithmetic, it may fail if you use the FPU to implement it.4
The conversion between packed BCD and the floating-point format is not a cheap operation. The fbld and fbstp instructions can be quite slow (more than two orders of magnitude slower than fld and fstp, for example). Therefore, these instructions can be costly if you’re doing simple additions or subtractions.
Because the FPU converts packed decimal values to the internal floating-point format, you can mix packed decimal, floating point, and (binary) integer formats in the same calculation. The following code fragment demonstrates how you might achieve this:
.data
tb tbyte 654321h
two real8 2.0
one dword 1
fbld tb
fmul two
fiadd one
fbstp tb
; TB now contains: 1308643h.The FPU treats packed decimal values as integer values. Therefore, if your calculations produce fractional results, the fbstp instruction will round the result according to the current FPU rounding mode. If you need to work with fractional values, you need to stick with floating-point results.
8.4 For More Information
Donald Knuth’s The Art of Computer Programming, Volume 2: Seminumerical Algorithms (Addison-Wesley Professional, 1997) contains a lot of useful information about decimal arithmetic and extended-precision arithmetic, though that text is generic and doesn’t describe how to do this in x86-64 assembly language. Additional information on BCD arithmetic can also be found at the following websites:
- BCD Arithmetic, a Tutorial, http://homepage.divms.uiowa.edu/~jones/bcd/bcd.html
- General Decimal Arithmetic, http://speleotrove.com/decimal/
- Intel Decimal Floating-Point Math Library, https://software.intel.com/en-us/articles/intel-decimal-floating-point-math-library/
8.5 Test Yourself
- Provide the code to compute x = y + z, assuming the following:
- x, y, and z are 128-bit integers
- x and y are 96-bit integers, and z is a 64-bit integer
- x, y, and z are 48-bit integers
- Provide the code to compute x = y − z, assuming the following:
- x, y, and z are 192-bit integers
- x, y, and z are 96-bit integers
- Provide the code to compute x = y × z, assuming x, y, and z are 128-bit unsigned integers.
- Provide the code to compute x = y / z, assuming x and y are 128-bit signed integers, and z is a 64-bit signed integer.
- Assuming x and y are unsigned 128-bit integers, convert the following to assembly language:
- if(x == y) then code
- if(x < y) then code
- if(x > y) then code
- if(x ≠ y) then code
- Assuming x and y are signed 96-bit integers, convert the following to assembly language:
- if(x == y) then code
- if(x < y) then code
- if(x > y) then code
- Assuming x and y are signed 128-bit integers, provide two distinct ways to convert the following to assembly language:
- x = –x
- x = –y
- Assuming x, y, and z are all 128-bit integer values, convert the following to assembly language:
- x = y & z (bitwise logical AND)
- x = y | z (bitwise logical OR)
- x = y ^ z (bitwise logical XOR)
- x = ~y (bitwise logical NOT)
- x = y << 1 (bitwise shift left)
- x = y >> 1 (bitwise shift right)
- Assuming x and y are signed 128-bit values, convert x = y >> 1 to assembly language (bitwise arithmetic shift right).
- Provide the assembly code to rotate the 128-bit value in x through the carry flag (left by 1 bit).
- Provide the assembly code to rotate the 128-bit value in x through the carry flag (right by 1 bit).