10
Table Lookups

This chapter discusses how to speed up or reduce the complexity of computations by using table lookups. Back in the early days of x86 programming, replacing expensive computations with table lookups was a common way to improve program performance. Today, memory speeds in modern systems limit performance gains that can be obtained by using table lookups. However, for complex calculations, this is still a viable technique for writing high-performance code. This chapter demonstrates the space/speed trade-offs when using table lookups.
10.1 Tables
To an assembly language programmer, a table is an array containing initialized values that do not change once created. In assembly language, you can use tables for a variety of purposes: computing functions, controlling program flow, or simply looking things up. In general, tables provide a fast mechanism for performing an operation at the expense of space in your program (the extra space holds the tabular data). In this section, we’ll explore some of the many possible uses of tables in an assembly language program.
10.1.1 Function Computation via Table Lookup
A simple-looking high-level-language arithmetic expression can be equivalent to a considerable amount of x86-64 assembly language code and, therefore, could be expensive to compute. Assembly language programmers often precompute many values and use a table lookup of those values to speed up their programs. This has the advantage of being easier, and it’s often more efficient as well.
Consider the following Pascal statement:
if (character >= 'a') and (character <= 'z') then
character := chr(ord(character) - 32);This Pascal if statement converts the character variable’s value from lowercase to uppercase if character is in the range a to z. The MASM code that does the same thing requires a total of seven machine instructions, as follows:
mov al, character
cmp al, 'a'
jb notLower
cmp al, 'z'
ja notLower
and al, 5fh ; Same as sub(32, al) in this code
mov character, al
notLower:Using a table lookup, however, allows you to reduce this sequence to just four instructions:
mov al, character
lea rbx, CnvrtLower
xlat
mov character, alThe xlat, or translate, instruction does the following:
mov al, [rbx + al * 1]This instruction uses the current value of the AL register as an index into the array whose base address is found in RBX. It fetches the byte at that index in the array and copies that byte into the AL register. Intel calls this instruction translate because programmers typically use it to translate characters from one form to another by using a lookup table, exactly the way we are using it here.
In the previous example, CnvrtLower is a 256-byte table that contains the values 0 to 60h at indices 0 to 60h, 41h to 5Ah at indices 61h to 7Ah, and 7Bh to 0FFh at indices 7Bh to 0FFh. Therefore, if AL contains a value in the range 0 to 60h or 7Ah to 0FFh, the xlat instruction returns the same value, effectively leaving AL unchanged. However, if AL contains a value in the range 61h to 7Ah (the ASCII codes for a to z), then the xlat instruction replaces the value in AL with a value in the range 41h to 5Ah (the ASCII codes for A to Z), thereby converting lowercase to uppercase.
As the complexity of a function increases, the performance benefits of the table-lookup method increase dramatically. While you would almost never use a lookup table to convert lowercase to uppercase, consider what happens if you want to swap cases; for example, via computation:
mov al, character
cmp al, 'a'
jb notLower
cmp al, 'z'
ja allDone
and al, 5fh
jmp allDone
notLower:
cmp al, 'A'
jb allDone
cmp al, 'Z'
ja allDone
or al, 20h
allDone:
mov character, alThis code has 13 machine instructions.
The table-lookup code to compute this same function is as follows:
mov al, character
lea rbx, SwapUL
xlat
mov character, alAs you can see, when using a table lookup to compute a function, only the table changes; the code remains the same.
10.1.1.1 Function Domains and Range
Functions computed via table lookup have a limited domain (the set of possible input values they accept), because each element in the domain of a function requires an entry in the lookup table. For example, our previous uppercase/lowercase conversion functions have the 256-character extended ASCII character set as their domain. A function such as sin or cos accepts the (infinite) set of real numbers as possible input values. You won’t find it very practical to implement a function via table lookup whose domain is the set of real numbers, because you must limit the domain to a small set.
Most lookup tables are quite small, usually 10 to 256 entries. Rarely do lookup tables grow beyond 1000 entries. Most programmers don’t have the patience to create (and verify the correctness) of a 1000-entry table (though see “Generating Tables” on page 590 for a discussion of generating tables programmatically).
Another limitation of functions based on lookup tables is that the elements in the domain must be fairly contiguous. Table lookups use the input value to a function as an index into the table, and return the value at that entry in the table. A function that accepts values 0, 100, 1000, and 10,000 would require 10,001 different elements in the lookup table because of the range of input values. Therefore, you cannot efficiently create such a function via a table lookup. Throughout this section on tables, we’ll assume that the domain of the function is a fairly contiguous set of values.
The range of a function is the set of possible output values it produces. From the perspective of a table lookup, a function’s range determines the size of each table entry. For example, if a function’s range is the integer values 0 through 255, then each table entry requires a single byte; if the range is 0 through 65,535, each table entry requires 2 bytes, and so on.
The best functions you can implement via table lookups are those whose domain and range are always 0 to 255 (or a subset of this range). Any such function can be computed using the same two instructions: lea rbx, table and xlat. The only thing that ever changes is the lookup table. The uppercase/lowercase conversion routines presented earlier are good examples of such a function.
You cannot (conveniently) use the xlat instruction to compute a function value once the range or domain of the function takes on values outside 0 to 255. There are three situations to consider:
- The domain is outside 0 to 255, but the range is within 0 to 255.
- The domain is inside 0 to 255, but the range is outside 0 to 255.
- Both the domain and range of the function take on values outside 0 to 255.
We will consider these cases in the following sections.
10.1.1.2 Domain Outside 0 to 255, Range Within 0 to 255
If the domain of a function is outside 0 to 255, but the range of the function falls within this set of values, our lookup table will require more than 256 entries, but we can represent each entry with a single byte. Therefore, the lookup table can be an array of bytes. Other than those lookups that can use the xlat instruction, functions falling into this class are the most efficient. The following Pascal function invocation
B := Func(X); where Func is
function Func(X:dword):byte; is easily converted to the following MASM code:
mov edx, X ; Zero-extends into RDX!
lea rbx, FuncTable
mov al, [rbx][rdx * 1]
mov B, alThis code loads the function parameter into RDX, uses this value (in the range 0 to ??) as an index into the FuncTable table, fetches the byte at that location, and stores the result into B. Obviously, the table must contain a valid entry for each possible value of X. For example, suppose you wanted to map a cursor position on an 80×25 text-based video display in the range 0 to 1999 (there are 2000 character positions on an 80×25 video display) to its X (0 to 79) or Y (0 to 24) coordinate on the screen. You could compute the X coordinate via the function
X = Posn % 80;and the Y coordinate with the formula
Y = Posn / 80;(where Posn is the cursor position on the screen). This can be computed using this x86-64 code:
mov ax, Posn
mov cl, 80
div cl
; X is now in AH, Y is now in AL.However, the div instruction on the x86-64 is very slow. If you need to do this computation for every character you write to the screen, you will seriously degrade the speed of your video-display code. The following code, which realizes these two functions via table lookup, may improve the performance of your code considerably:
lea rbx, yCoord
movzx ecx, Posn ; Use a plain mov instr if Posn
mov al, [rbx][rcx * 1] ; is uns32 rather than an
lea rbx, xCoord ; uns16 value
mov ah, [rbx][rcx * 1]Keep in mind that loading a value into ECX automatically zero-extends that value into RCX. Therefore, the movzx instruction in this code sequence actually zero-extends Posn into RCX, not just ECX.
If you’re willing to live with the limitations of the LARGEADDRESSAWARE:NO linking option (see “Large Address Unaware Applications” in Chapter 3), you can simplify this code somewhat:
movzx ecx, Posn ; Use a plain mov instr if Posn
mov al, yCoord[rcx * 1] ; is uns32 rather than an
mov ah, xCoord[rcx * 1] ; uns16 value10.1.1.3 Domain in 0 to 255 and Range Outside 0 to 255, or Both Outside 0 to 255
If the domain of a function is within 0 to 255, but the range is outside this set, the lookup table will contain 256 or fewer entries, but each entry will require 2 or more bytes. If both the range and domains of the function are outside 0 to 255, each entry will require 2 or more bytes and the table will contain more than 256 entries.
Recall from Chapter 4 that the formula for indexing into a single-dimensional array (of which a table is a special case) is as follows:
element_address = Base + index * element_sizeIf elements in the range of the function require 2 bytes, you must multiply the index by 2 before indexing into the table. Likewise, if each entry requires 3, 4, or more bytes, the index must be multiplied by the size of each table entry before being used as an index into the table. For example, suppose you have a function, F(x), defined by the following (pseudo) Pascal declaration:
function F(x:dword):word;You can create this function by using the following x86-64 code (and, of course, the appropriate table named F):
movzx ebx, x
lea r8, F
mov ax, [r8][rbx * 2]If you can live with the limitations of LARGEADDRESSAWARE:NO, you can reduce this as follows:
movzx ebx, x
mov ax, F[rbx * 2]Any function whose domain is small and mostly contiguous is a good candidate for computation via table lookup. In some cases, noncontiguous domains are acceptable as well, as long as the domain can be coerced into an appropriate set of values (an example you’ve already seen is processing switch statement expressions). Such operations, called conditioning, are the subject of the next section.
10.1.1.4 Domain Conditioning
Domain conditioning is taking a set of values in the domain of a function and massaging them so that they are more acceptable as inputs to that function. Consider the following function:
sin x = sin x|(x∈[–2π,2π])This says that the (computer) function sin(x) is equivalent to the (mathematical) function sin x where
–2π <= x <= 2πAs we know, sine is a circular function, which will accept any real-value input. The formula used to compute sine, however, accepts only a small set of these values.
This range limitation doesn’t present any real problems; by simply computing sin(x mod (2 * pi)), we can compute the sine of any input value. Modifying an input value so that we can easily compute a function is called conditioning the input. In the preceding example, we computed x mod 2 * pi and used the result as the input to the sin function. This truncates x to the domain sin needs without affecting the result. We can apply input conditioning to table lookups as well. In fact, scaling the index to handle word entries is a form of input conditioning. Consider the following Pascal function:
function val(x:word):word; begin
case x of
0: val := 1;
1: val := 1;
2: val := 4;
3: val := 27;
4: val := 256;
otherwise val := 0;
end;
end; This function computes a value for x in the range 0 to 4 and returns 0 if x is outside this range. Since x can take on 65,536 different values (being a 16-bit word), creating a table containing 65,536 words where only the first five entries are nonzero seems to be quite wasteful. However, we can still compute this function by using a table lookup if we use input conditioning. The following assembly language code presents this principle:
mov ax, 0 ; AX = 0, assume x > 4
movzx ebx, x ; Note that HO bits of RBX must be 0!
lea r8, val
cmp bx, 4
ja defaultResult
mov ax, [r8][rbx * 2]
defaultResult:This code checks to see if x is outside the range 0 to 4. If so, it manually sets AX to 0; otherwise, it looks up the function value through the val table. With input conditioning, you can implement several functions that would otherwise be impractical to do via table lookup.
10.1.2 Generating Tables
One big problem with using table lookups is creating the table in the first place. This is particularly true if the table has many entries. Figuring out the data to place in the table, then laboriously entering the data and, finally, checking that data to make sure it is valid, is very time-consuming and boring. For many tables, there is no way around this process. For other tables, there is a better way: using the computer to generate the table for you.
An example is probably the best way to describe this. Consider the following modification to the sine function:
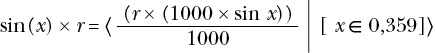
This states that x is an integer in the range 0 to 359 and r must be an integer. The computer can easily compute this with the following code:
Thousand dword 1000
.
.
.
lea r8, Sines
movzx ebx, x
mov eax, [r8][rbx * 2] ; Get sin(x) * 1000
imul r ; Note that this extends EAX into EDX
idiv Thousand ; Compute (r *(sin(x) * 1000)) / 1000(This provides the usual improvement if you can live with the limitations of LARGEADDRESSAWARE:NO.)
Note that integer multiplication and division are not associative. You cannot remove the multiplication by 1000 and the division by 1000 because they appear to cancel each other out. Furthermore, this code must compute this function in exactly this order.
All that we need to complete this function is Sines, a table containing 360 different values corresponding to the sine of the angle (in degrees) times 1000. The C/C++ program in Listing 10-1 generates this table for you.
// Listing 10-1: GenerateSines
// A C program that generates a table of sine values for
// an assembly language lookup table.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
int main(int argc, char **argv)
{
FILE *outFile;
int angle;
int r;
// Open the file:
outFile = fopen("sines.asm", "w");
// Emit the initial part of the declaration to
// the output file:
fprintf
(
outFile,
"Sines:" // sin(0) = 0
);
// Emit the sines table:
for(angle = 0; angle <= 359; ++angle)
{
// Convert angle in degrees to an angle in
// radians using:
// radians = angle * 2.0 * pi / 360.0;
// Multiply by 1000 and store the rounded
// result into the integer variable r.
double theSine =
sin
(
angle * 2.0 *
3.14159265358979323846 /
360.0
);
r = (int) (theSine * 1000.0);
// Write out the integers eight per line to the
// source file.
// Note: If (angle AND %111) is 0, then angle
// is divisible by 8 and we should output a
// newline first.
if((angle & 7) == 0)
{
fprintf(outFile, "\n\tword\t");
}
fprintf(outFile, "%5d", r);
if ((angle & 7) != 7)
{
fprintf(outFile, ",");
}
} // endfor
fprintf(outFile, "\n");
fclose(outFile);
return 0;
} // end mainListing 10-1: A C program that generates a table of sines
This program produces the following output (truncated for brevity):
Sines:
word 0, 17, 34, 52, 69, 87, 104, 121
word 139, 156, 173, 190, 207, 224, 241, 258
word 275, 292, 309, 325, 342, 358, 374, 390
word 406, 422, 438, 453, 469, 484, 499, 515
word 529, 544, 559, 573, 587, 601, 615, 629
word 642, 656, 669, 681, 694, 707, 719, 731
word 743, 754, 766, 777, 788, 798, 809, 819
word 829, 838, 848, 857, 866, 874, 882, 891
word 898, 906, 913, 920, 927, 933, 939, 945
word 951, 956, 961, 965, 970, 974, 978, 981
word 984, 987, 990, 992, 994, 996, 997, 998
word 999, 999, 1000, 999, 999, 998, 997, 996
word 994, 992, 990, 987, 984, 981, 978, 974
word 970, 965, 961, 956, 951, 945, 939, 933
word 927, 920, 913, 906, 898, 891, 882, 874
.
.
.
word -898, -891, -882, -874, -866, -857, -848, -838
word -829, -819, -809, -798, -788, -777, -766, -754
word -743, -731, -719, -707, -694, -681, -669, -656
word -642, -629, -615, -601, -587, -573, -559, -544
word -529, -515, -500, -484, -469, -453, -438, -422
word -406, -390, -374, -358, -342, -325, -309, -292
word -275, -258, -241, -224, -207, -190, -173, -156
word -139, -121, -104, -87, -69, -52, -34, -17Obviously, it’s much easier to write the C program that generated this data than to enter (and verify) this data by hand. Of course, you don’t even have to write the table-generation program in C (or Pascal/Delphi, Java, C#, Swift, or another high-level language). Because the program will execute only once, the performance of the table-generation program is not an issue.
Once you run your table-generation program, all that remains to be done is to cut and paste the table from the file (sines.asm in this example) into the program that will actually use the table.
10.1.3 Table-Lookup Performance
In the early days of PCs, table lookups were a preferred way to do high-performance computations. Today, it is not uncommon for a CPU to be 10 to 100 times faster than main memory. As a result, using a table lookup may not be faster than doing the same calculation with machine instructions. However, the on-chip CPU cache memory subsystems operate at near CPU speeds. Therefore, table lookups can be cost-effective if your table resides in cache memory on the CPU. This means that the way to get good performance using table lookups is to use small tables (because there’s only so much room on the cache) and use tables whose entries you reference frequently (so the tables stay in the cache).
See Write Great Code, Volume 1 (No Starch Press, 2020) or the electronic version of The Art of Assembly Language at https://www.randallhyde.com/ for details concerning the operation of cache memory and how you can optimize your use of cache memory.
10.2 For More Information
Donald Knuth’s The Art of Computer Programming, Volume 3: Searching and Sorting (Addison-Wesley Professional, 1998) contains a lot of useful information about searching for data in tables. Searching for data is an alternative when a straight array access won’t work in a given situation.
10.3 Test Yourself
- What is the domain of a function?
- What is the range of a function?
- What does the
xlatinstruction do? - Which domain and range values allow you to use the
xlatinstruction? - Provide the code that implements the following functions (using pseudo-C prototypes and
fas the table name):byte f(byte input)word f(byte input)byte f(word input)word f(word input)
- What is domain conditioning?
- Why might table lookups not be effective on modern processors?