12
Bit Manipulation

Manipulating bits in memory is, perhaps, the feature for which assembly language is most famous. Even the C programming language, known for bit manipulation, doesn’t provide as complete a set of bit-manipulation operations.
This chapter discusses how to manipulate strings of bits in memory and registers by using x86-64 assembly language. It begins with a review of the bit-manipulation instructions covered thus far, introduces a few new instructions, then reviews information on packing and unpacking bit strings in memory, which is the basis for many bit-manipulation operations. Finally, this chapter discusses several bit-centric algorithms and their implementation in assembly language.
12.1 What Is Bit Data, Anyway?
Bit manipulation refers to working with bit data: data types that consist of strings of bits that are noncontiguous or not a multiple of 8 bits long. Generally, such bit objects will not represent numeric integers, although we will not place this restriction on our bit strings.
A bit string is a contiguous sequence of 1 or more bits. It does not have to start or end at any special point. For example, a bit string could start in bit 7 of a byte in memory and continue through to bit 6 of the next byte in memory. Likewise, a bit string could begin in bit 30 of EAX, consume the upper 2 bits of EAX, and then continue from bit 0 through bit 17 of EBX. In memory, the bits must be physically contiguous (that is, the bit numbers are always increasing except when crossing a byte boundary, and at byte boundaries the memory address increases by 1 byte). In registers, if a bit string crosses a register boundary, the application defines the continuation register, but the bit string always continues in bit 0 of that second register.
A bit run is a sequence of bits with all the same value. A run of zeros is a bit string that contains all 0s, and a run of ones is a bit string containing all 1s. The first set bit in a bit string is the bit position of the first bit containing a 1 in a bit string; that is, the first 1 bit following a possible run of zeros. A similar definition exists for the first clear bit. The last set bit is the last bit position in a bit string that contains 1s; the remainder of the string forms an uninterrupted run of zeros. A similar definition exists for the last clear bit.
A bit set is a collection of bits, not necessarily contiguous, within a larger data structure. For example, bits 0 to 3, 7, 12, 24, and 31 from a double word form a set of bits. Normally, we will deal with bit sets that are part of a container object (the data structure that encapsulates the bit set) no more than about 32 or 64 bits in size, though this limit is completely artificial. Bit strings are special cases of bit sets.
A bit offset is the number of bits from a boundary position (usually a byte boundary) to the specified bit. As noted in Chapter 2, we number the bits starting from 0 at the boundary location.
A mask is a sequence of bits that we’ll use to manipulate certain bits in another value. For example, the bit string 0000_1111_0000b, when it’s used with the and instruction, masks away (clears) all the bits except bits 4 through 7. Likewise, if you use the same value with the or instruction, it can set bits 4 through 7 in the destination operand. The term mask comes from the use of these bit strings with the and instruction. In those situations, the 1 and 0 bits behave like masking tape when you’re painting something; they pass through certain bits unchanged while masking out (clearing) the other bits.
Armed with these definitions, we’re ready to start manipulating some bits!
12.2 Instructions That Manipulate Bits
Bit manipulation generally consists of six activities: setting bits, clearing bits, inverting bits, testing and comparing bits, extracting bits from a bit string, and inserting bits into a bit string. The most basic bit-manipulation instructions are the and, or, xor, not, test, and shift and rotate instructions. The following paragraphs review these instructions, concentrating on how you could use them to manipulate bits in memory or registers.
12.2.1 The and Instruction
The and instruction provides the ability to replace unwanted bits in a bit sequence with 0s. This instruction is especially useful for isolating a bit string or a bit set that is merged with other, unrelated data (or, at least, data that is not part of the bit string or bit set). For example, suppose that a bit string consumes bit positions 12 through 24 of the EAX register; we can isolate this bit string by setting all other bits in EAX to 0 by using the following instruction (see Figure 12-1):
and eax, 1111111111111000000000000b In theory, you could use the or instruction to mask all unwanted bits to 1s rather than 0s, but later comparisons and operations are often easier if the unneeded bit positions contain 0.
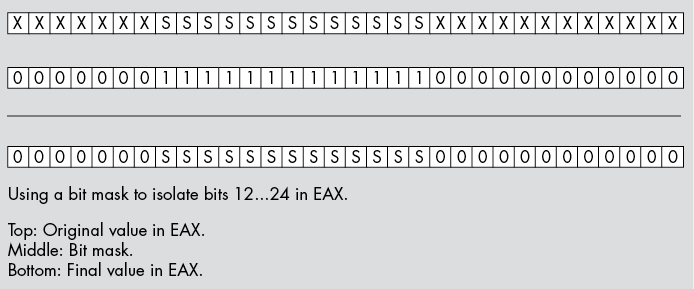
Figure 12-1: Isolating a bit string by using the and instruction
Once you’ve cleared the unneeded bits in a set of bits, you can often operate on the bit set in place. For example, to see if the string of bits in positions 12 through 24 of EAX contains 12F3h, you could use the following code:
and eax, 1111111111111000000000000b
cmp eax, 1001011110011000000000000b Here’s another solution, using constant expressions, that’s a little easier to digest:
and eax, 1111111111111000000000000b
cmp eax, 12F3h shl 12To make the constants and other values you use in conjunction with this value easier to deal with, you can use the shr instruction to align the bit string with bit 0 after you’ve masked it, like this:
and eax, 1111111111111000000000000b
shr eax, 12
cmp eax, 12F3h
Other operations that require the bit string at bit #0 12.2.2 The or Instruction
The or instruction is especially useful for inserting a bit set into another bit string, using the following steps:
- Clear all the bits surrounding your bit set in the source operand.
- Clear all the bits in the destination operand where you wish to insert the bit set.
- OR the bit set and destination operand together.
For example, suppose you have a value in bits 0 to 12 of EAX that you wish to insert into bits 12 to 24 of EBX without affecting any of the other bits in EBX. You would begin by stripping out bits 13 and above from EAX; then you would strip out bits 12 to 24 in EBX. Next, you would shift the bits in EAX so the bit string occupies bits 12 to 24 of EAX. Finally, you would OR the value in EAX into EBX (see Figure 12-2), as shown here:
and eax, 1FFFh ; Strip all but bits 0 to 12 from EAX
and ebx, 0FE000FFFh ; Clear bits 12 to 24 in EBX
shl eax, 12 ; Move bits 0 to 12 to 12 to 24 in EAX
or ebx,eax ; Merge the bits into EBXIn Figure 12-2, the desired bits (AAAAAAAAAAAAA) form a bit string. However, this algorithm still works fine even if you’re manipulating a noncontiguous set of bits. All you have to do is to create a bit mask that has 1s in the appropriate places.
When you work with bit masks, it is incredibly poor programming style to use literal numeric constants as in the past few examples. You should always create symbolic constants in MASM. By combining these with some constant expressions, you can produce code that is much easier to read and maintain. The current example code is more properly written as the following:
StartPosn = 12
BitMask = 1FFFh shl StartPosn ; Mask occupies bits 12 to 24
.
.
.
shl eax, StartPosn ; Move into position
and eax, BitMask ; Strip all but bits 12 to 24 from EAX
and ebx, not BitMask ; Clear bits 12 to 24 in EBX
or ebx, eax ; Merge the bits into EBX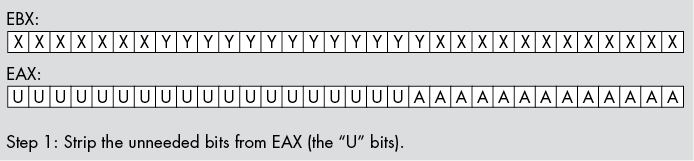
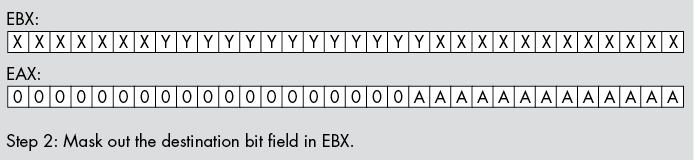

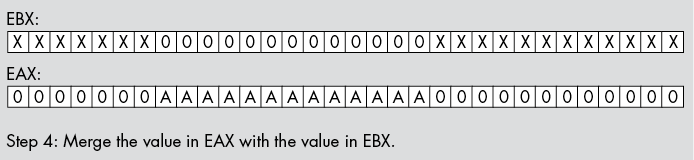

Figure 12-2: Inserting bits 0 to 12 of EAX into bits 12 to 24 of EBX
The use of the compile time not operator to invert the bit mask saves having to create another constant in the program that has to be changed anytime you modify the BitMask constant. Having to maintain two separate symbols whose values are dependent on one another is not a good thing in a program.
Of course, in addition to merging one bit set with another, the or instruction is also useful for forcing bits to 1 in a bit string. By setting various bits in a source operand to 1, you can force the corresponding bits in the destination operand to 1 by using the or instruction.
12.2.3 The xor Instruction
The xor instruction allows you to invert selected bits in a bit set. Of course, if you want to invert all the bits in a destination operand, the not instruction is more appropriate; however, if you want to invert selected bits while not affecting others, xor is the way to go.
One interesting fact about xor’s operation is that it lets you manipulate known data in just about any way imaginable. For example, if you know that a field contains 1010b, you can force that field to 0 by XORing it with 1010b. Similarly, you can force it to 1111b by XORing it with 0101b. Although this might seem like a waste, because you can easily force this 4-bit string to 0 or all 1s by using and/or, the xor instruction has two advantages. First, you are not limited to forcing the field to all 0s or all 1s; you can actually set these bits to any of the 16 valid combinations via xor. Second, if you need to manipulate other bits in the destination operand at the same time, and/or may not be able to do the job.
For example, suppose you know that one field contains 1010b that you want to force to 0, and another field in the same operand contains 1000b and you wish to increment that field by 1 (that is, set the field to 1001b). You cannot accomplish both operations with a single and or or instruction, but you can with a single xor instruction; just XOR the first field with 1010b and the second field with 0001b. Remember, however, that this trick works only if you know the current value of a bit set within the destination operand.
12.2.4 Flag Modification by Logical Instructions
In addition to setting, clearing, and inverting bits in a destination operand, the and, or, and xor instructions also affect various condition codes in the FLAGS register. These instructions do the following:
- Always clear the carry and overflow flags.
- Set the sign flag if the result has a 1 in the HO bit. They clear it otherwise; that is, these instructions copy the HO bit of the result into the sign flag.
- Set or clear the zero flag if the result is zero or not zero, respectively.
- Set the parity flag if there is an even number of set bits in the LO byte of the destination operand, and clear the parity flag if there is an odd number of set bits.
Because these instructions always clear the carry and overflow flags, you cannot expect the system to preserve the state of these two flags across the execution of these instructions. A common mistake in many assembly language programs is the assumption that these instructions do not affect the carry flag. Many people will execute an instruction that sets or clears the carry flag; execute an and, or, or xor instruction; and then attempt to test the state of the carry from the previous instruction. This simply will not work.
One of the more interesting aspects to these instructions is that they copy the HO bit of their result into the sign flag. Therefore, you can easily test the HO bit by testing the sign flag (using cmovs and cmovns, sets and setns, or js and jns instructions). For this reason, many assembly language programmers will place an important Boolean variable in the HO bit of an operand so they can easily test the state of that variable by using the sign flag after a logical operation.
12.2.4.1 The Parity Flag
Parity is a simple error-detection scheme originally employed by telegraphs and other serial communication protocols. The idea was to count the number of set bits in a character and include an extra bit in the transmission to indicate whether that character contained an even or odd number of set bits. The receiving end of the transmission would also count the bits and verify that the extra parity bit indicated a successful transmission. The purpose of the parity flag is to help compute the value of this extra bit, though parity-checking has been taken over by hardware.1
The x86-64 and, or, and xor instructions set the parity bit if the LO byte of their operand contains an even number of set bits. An important fact bears repeating here: the parity flag reflects only the number of set bits in the LO byte of the destination operand; it does not include the HO bytes in a word, double-word, or other-sized operand. The instruction set uses the LO byte only to compute the parity because communication programs that use parity are typically character-oriented transmission systems (better error-checking schemes could be used if you transmit more than 8 bits at a time).
12.2.4.2 The Zero Flag
The zero flag setting is one of the more important results produced by the and, or, and xor instructions. Indeed, programs reference this flag so often after the and instruction that Intel added a separate instruction, test, whose main purpose is to logically AND two results and set the flags without otherwise affecting either instruction operand.
The zero flag has three main uses after the execution of an and or a test instruction: (1) checking to see if a particular bit in an operand is set, (2) checking to see if at least one of several bits in a bit set is 1, and (3) checking to see if an operand is 0. Using (1) is actually a special case of (2), in which the bit set contains only a single bit. We’ll explore each of these uses in the following paragraphs.
To test whether a particular bit is set in a given operand, use the and and test instructions for an operand with a constant value containing a single set bit you wish to test. This clears all the other bits in the operand, leaving a 0 in the bit position under test if the operand contained a 0 in that bit position and a 1 if it contained a 1. Because all of the other bits in the result are 0, the entire result will be 0 if that particular bit is 0; the entire result will be nonzero if that bit position contains a 1. The x86-64 reflects this status in the zero flag (Z = 1 indicates a 0 bit; Z = 0 indicates a 1 bit). The following instruction sequence demonstrates how to test if bit 4 is set in EAX:
test eax, 10000b ; Check bit #4 to see if it is 0 or 1
jnz bitIsSet
Do this if the bit is clear
.
.
.
bitIsSet: ; Branch here if the bit is setYou can also use the and and test instructions to see if any one of several bits is set. Simply supply a constant that has a 1 in all the positions you want to test (and 0s everywhere else). ANDing an operand with such a constant will produce a nonzero value if one or more of the bits in the operand under test contain a 1. The following example tests whether the value in EAX contains a 1 in bit positions 1, 2, 4, and 7:
test eax, 10010110b
jz noBitsSet
Do whatever needs to be done if one of the bits is set
noBitsSet: You cannot use a single and or test instruction to see if all the corresponding bits in the bit set are equal to 1. To accomplish this, you must first mask out the bits that are not in the set and then compare the result against the mask itself. If the result is equal to the mask, all the bits in the bit set contain 1s. You must use the and instruction for this operation because the test instruction does not modify the result. The following example checks whether all the bits in a bit set (bitMask) are equal to 1:
and eax, bitMask
cmp eax, bitMask
jne allBitsArentSet
; All the bit positions in EAX corresponding to the set
; bits in bitMask are equal to 1 if we get here.
Do whatever needs to be done if the bits match
allBitsArentSet: Of course, once we stick the cmp instruction in there, we don’t really have to check whether all the bits in the bit set contain 1s. We can check for any combination of values by specifying the appropriate value as the operand to the cmp instruction.
Note that the test and and instructions will set the zero flag in the preceding code sequences only if all the bits in EAX (or other destination operand) have 0s in the positions where 1s appear in the constant operand. This suggests another way to check for all 1s in the bit set: invert the value in EAX prior to using the and or test instruction. Then if the zero flag is set, you know that there were all 1s in the (original) bit set. For example:
not eax
test eax, bitMask
jnz NotAllOnes
; At this point, EAX contained all 1s in the bit positions
; occupied by 1s in the bitMask constant.
Do whatever needs to be done at this point
NotAllOnes: The previous paragraphs all suggest that the bitMask (the source operand) is a constant, but you can use a variable or other register too. Simply load that variable or register with the appropriate bit mask before you execute the test, and, or cmp instructions in the preceding examples.
12.2.5 The Bit Test Instructions
Another set of instructions we’ve already seen that we can use to manipulate bits is the bit test instructions. These instructions include bt (bit test), bts (bit test and set), btc (bit test and complement), and btr (bit test and reset). The btx instructions use the following syntax:
btx bits_to_test, bit_number
btx reg16, reg16
btx reg32, reg32
btx reg64, reg64
btx reg16, constant
btx reg32, constant
btx reg64, constant
btx mem16, reg16
btx mem32, reg32
btx mem64, reg64
btx mem16, constant
btx mem32, constant
btx mem64, constantwhere x is nothing, c, s, or r.
The btx instructions’ second operand is a bit number that specifies which bit to check in the first operand. If the first operand is a register, the second operand must contain a value between 0 and the size of the register (in bits) minus 1; because the x86-64’s largest (general-purpose) registers are 64 bits, this value has the maximum value of 63 (for 64-bit registers). If the first operand is a memory location, the bit count is not limited to values in the range 0 to 63. If the second operand is a constant, it can be any 8-bit value in the range 0 to 255. If the second operand is a register, it has no (practical) limitation and, in fact, it allows negative bit offsets.
The bt instruction copies the specified bit from the second operand into the carry flag. For example, the bt eax, 8 instruction copies bit 8 of the EAX register into the carry flag. You can test the carry flag after this instruction to determine whether bit 8 was set or clear in EAX.
The bts, btc, and btr instructions manipulate the bit they test while they are testing it. These instructions may be slow (depending on the processor you’re using), and you should avoid them if performance is your primary concern, particularly if you’re using an older CPU. If performance (versus convenience) is an issue, you should always try two different algorithms—one that uses these instructions, and one that uses and and or instructions—and measure the performance difference; then choose the best of the two approaches.
12.2.6 Manipulating Bits with Shift and Rotate Instructions
The shift and rotate instructions are another group of instructions you can use to manipulate and test bits. These instructions move the HO (left shift and rotate) or LO (right shift and rotate) bits into the carry flag. Therefore, you can test the carry flag after you execute one of these instructions to determine the original setting of the operand’s HO or LO bit; for example:
shr al, 1
jc LOBitWasSetThe nice thing about the shift and rotate instructions is that they automatically move bits up or down in their operand so the next bit to test is in place; this is especially useful when operating within a loop.
The shift and rotate instructions are invaluable for aligning bit strings and packing and unpacking data. Chapter 2 has several examples of this, and some earlier examples in this chapter also use the shift instructions for this purpose.
12.3 The Carry Flag as a Bit Accumulator
The btx, shift, and rotate instructions set or clear the carry flag depending on the operation and selected bit. Because these instructions place their “bit result” in the carry flag, it is often convenient to think of the carry flag as a 1-bit register or accumulator for bit operations. In this section, we will explore some of the operations possible with this bit result in the carry flag.
Instructions that use the carry flag as some sort of input value are useful for manipulating bit results in the carry flag. For example:
adc,sbbrcl,rcrcmc,clc, andstccmovc,cmovncjc,jncsetc,setnc
The adc and sbb instructions add or subtract their operands along with the carry flag, so if you’ve computed a bit result into the carry flag, you can figure that result into an addition or a subtraction by using these instructions.
To save a carry flag result, you can use the rotate-through-carry instructions (rcl and rcr), which move the carry flag into the LO or HO bits of their destination operand. These instructions are useful for packing a set of bit results into a byte, word, or double-word value.
The cmc (complement carry) instruction lets you easily invert the result of a bit operation. You can also use the clc and stc instructions to initialize the carry flag prior to a string of bit operations involving the carry flag.
Instructions that test the carry flag, like jc, jnc, cmovc, cmovnc, setc, and setnc, are useful after a calculation that leaves a bit result in the carry flag.
If you have a sequence of bit calculations and would like to test whether those calculations produce a specific set of 1-bit results, you can clear a register or memory location and use the rcl or rcr instruction to shift each result into that location. Once the bit operations are complete, compare the register or memory location, holding the result against a constant value. If you want to test a sequence of results involving ANDs and ORs, you could use the setc and setnc instruction to set a register to 0 or 1 and then use the and and or instructions to merge the results.
12.4 Packing and Unpacking Bit Strings
A common bit operation is inserting a bit string into an operand or extracting a bit string from an operand. Chapter 2 provided simple examples of packing and unpacking such data; now it is time to formally describe how to do this.
For our purposes, I will assume that we’re dealing with bit strings that fit within a byte, word, double-word, or quad-word operand. Large bit strings that cross object boundaries require additional processing; we’ll discuss bit strings that cross quad-word boundaries later in this section.
When packing and unpacking a bit string, we must consider its starting bit position and length. The starting bit position is the bit number of the LO bit of the string in the larger operand. The length is the number of bits in the operand.
To insert (pack) data into a destination operand, you start with a bit string of the appropriate length that is right-justified (starts in bit position 0) and zero-extended to 8, 16, 32, or 64 bits; then insert this data at the appropriate starting position in another operand that is 8, 16, 32, or 64 bits wide. There is no guarantee that the destination bit positions contain any particular value.
The first two steps (which can occur in any order) are to clear out the corresponding bits in the destination operand and to shift (a copy of) the bit string so that the LO bit begins at the appropriate bit position. The third step is to OR the shifted result with the destination operand. This inserts the bit string into the destination operand (see Figure 12-3).
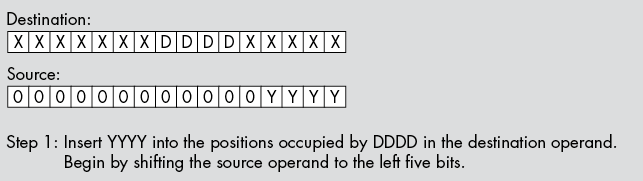
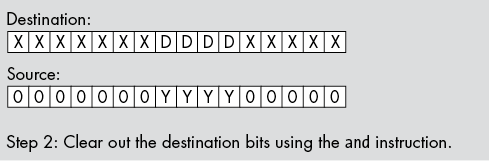
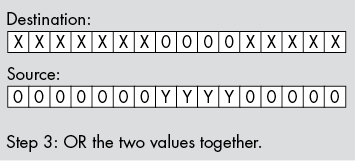
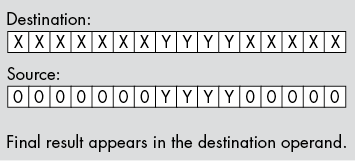
Figure 12-3: Inserting a bit string into a destination operand
The following three instructions insert a bit string of known length into a destination operand, as shown in Figure 12-3. These instructions assume that the source operand is in BX and the destination operand is in AX:
shl bx, 5
and ax, 1111111000011111b
or ax, bx If the length and the starting position aren’t known when you’re writing the program (that is, you have to calculate them at runtime), then you can use a lookup table to insert a bit string. Let’s assume that we have two 8-bit values: a starting bit position for the field we’re inserting and a nonzero 8-bit length value. Also assume that the source operand is in EBX and the destination operand is in EAX. The mergeBits procedure in Listing 12-1 demonstrates how to do this.
; Listing 12-1
; Demonstrate inserting bit strings into a register.
; Note that this program must be assembled and linked
; with the "LARGEADDRESSAWARE:NO" option.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 12-1", 0
; The index into the following table specifies the length
; of the bit string at each position. There are 65 entries
; in this table (one for each bit length from 0 to 64).
.const
MaskByLen equ this qword
qword 0
qword 1, 3, 7, 0fh
qword 1fh, 3fh, 7fh, 0ffh
qword 1ffh, 3ffh, 7ffh, 0fffh
qword 1fffh, 3fffh, 7fffh, 0ffffh
qword 1ffffh, 3ffffh, 7ffffh, 0fffffh
qword 1fffffh, 3fffffh, 7fffffh, 0ffffffh
qword 1ffffffh, 3ffffffh, 7ffffffh, 0fffffffh
qword 1fffffffh, 3fffffffh, 7fffffffh, 0ffffffffh
qword 1ffffffffh, 03ffffffffh
qword 7ffffffffh, 0fffffffffh
qword 1fffffffffh, 03fffffffffh
qword 7fffffffffh, 0ffffffffffh
qword 1ffffffffffh, 03ffffffffffh
qword 7ffffffffffh, 0fffffffffffh
qword 1fffffffffffh, 03fffffffffffh
qword 7fffffffffffh, 0ffffffffffffh
qword 1ffffffffffffh, 03ffffffffffffh
qword 7ffffffffffffh, 0fffffffffffffh
qword 1fffffffffffffh, 03fffffffffffffh
qword 7fffffffffffffh, 0ffffffffffffffh
qword 1ffffffffffffffh, 03ffffffffffffffh
qword 7ffffffffffffffh, 0fffffffffffffffh
qword 1fffffffffffffffh, 03fffffffffffffffh
qword 7fffffffffffffffh, 0ffffffffffffffffh
Val2Merge qword 12h, 1eh, 5555h, 1200h, 120h
LenInBits byte 5, 9, 16, 16, 12
StartPosn byte 7, 4, 4, 12, 18
MergeInto qword 0ffffffffh, 0, 12345678h
qword 11111111h, 0f0f0f0fh
include getTitle.inc
include print.inc
.code
; mergeBits(Val2Merge, MergeWith, Start, Length):
; Length (LenInBits[i]) value is passed in DL.
; Start (StartPosn[i]) is passed in CL.
; Val2Merge (Val2Merge[i]) and MergeWith (MergeInto[i])
; are passed in RBX and RAX.
; mergeBits result is returned in RAX.
mergeBits proc
push rbx
push rcx
push rdx
push r8
movzx edx, dl ; Zero-extends to RDX
mov rdx, MaskByLen[rdx * 8]
shl rdx, cl
not rdx
shl rbx, cl
and rax, rdx
or rax, rbx
pop r8
pop rdx
pop rcx
pop rbx
ret
mergeBits endp
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbx
push rsi
push rdi
push rbp
mov rbp, rsp
sub rsp, 56 ; Shadow storage
; The following loop calls mergeBits as
; follows:
; mergeBits(Val2Merge[i], MergeInto[i],
; StartPosn[i], LenInBits[i]);
; Where "i" runs from 4 down to 0.
; Index of the last element in the arrays:
mov r10, (sizeof LenInBits) - 1
testLoop:
; Fetch the Val2Merge element and write
; its value to the display while it is handy.
mov rdx, Val2Merge[r10 * 8]
call print
byte "merge( %x, ", 0
mov rbx, rdx
; Fetch the MergeInto element and write
; its value to the display.
mov rdx, MergeInto[r10 * 8]
call print
byte "%x, ", 0
mov rax, rdx
; Fetch the StartPosn element and write
; its value to the display.
movzx edx, StartPosn[r10 * 1] ; Zero-extends to RDX
call print
byte "%d, ", 0
mov rcx, rdx
; Fetch the LenInBits element and write
; its value to the display.
movzx edx, LenInBits[r10 * 1] ; Zero-extends to RDX
call print
byte "%d ) = ", 0
; Call mergeBits(Val2Merge, MergeInto,
; StartPosn, LenInBits)
call mergeBits
; Display the function result (returned
; in RAX). For this program, the results
; are always 32 bits, so it prints only
; the LO 32 bits of RAX:
mov edx, eax
call print
byte "%x", nl, 0
; Repeat for each element of the array.
dec r10
jns testLoop
allDone: leave
pop rdi
pop rsi
pop rbx
ret ; Returns to caller
asmMain endp
endListing 12-1: Inserting bits where the bit string length and starting position are variables
Here’s the build command and output for the program in Listing 12-1. Because this program accesses arrays directly (rather than loading their addresses into registers, which obfuscates the code), this program must be built with the LARGEADDRESSAWARE:NO flag, hence the use of the sbuild.bat batch file (see the description of sbuild.bat in “Large Address Unaware Applications” in Chapter 3):
C:\>sbuild listing12-1
C:\>echo off
Assembling: listing12-1.asm
c.cpp
C:\>listing12-1
Calling Listing 12-1:
merge(120, f0f0f0f, 18, 12) = 4830f0f
merge(1200, 11111111, 12, 16) = 11200111
merge(5555, 12345678, 4, 16) = 12355558
merge(1e, 0, 4, 9) = 1e0
merge(12, ffffffff, 7, 5) = fffff97f
Listing 12-1 terminatedEach entry in the MaskByLen table (in Listing 12-1) contains the number of 1 bits specified by the index into the table. Using the mergeBits Length parameter value as an index into this table fetches a value that has as many 1 bits as the Length value. The mergeBits function fetches an appropriate mask, shifts it to the left so that the LO bit of this run of 1s matches the starting position of the field into which we want to insert the data, and then inverts the mask and uses the inverted value to clear the appropriate bits in the destination operand.
To extract a bit string from a larger operand, all you have to do is mask out the unwanted bits and then shift the result until the LO bit of the bit string is in bit 0 of the destination operand. For example, to extract the 4-bit field starting at bit position 5 in EBX and leave the result in EAX, you could use the following code:
mov eax, ebx ; Copy data to destination
and eax, 111100000b ; Strip unwanted bits
shr eax, 5 ; Right-justify to bit position 0If you do not know the bit string’s length and starting position when you’re writing the program, you can still extract the desired bit string. The code is similar to insertion (though a little simpler). Assuming you have the Length and Start values we used when inserting a bit string, you can extract the corresponding bit string by using the following code (assuming source = EBX and dest = EAX):
movzx edx, Length
lea r8, MaskByLen ; Table from Listing 12-1
mov rdx, [r8][rdx * 8]
mov cl, StartingPosition
mov rax, rbx
shr rax, cl
and rax, rdxThe examples up to this point all assume that the bit string appears completely within a quad-word (or smaller) object. This will always be the case if the bit string is less than or equal to 64 bits in length. However, if the length of the bit string plus its starting position (modulo 8) within an object is greater than 64, the bit string will cross a quad-word boundary within the object.
Extracting such bit strings requires up to three operations: one operation to extract the start of the bit string (up to the first quad-word boundary), an operation that copies whole quad words (assuming the bit string is so long that it consumes several quad words), and a final operation that copies leftover bits in the last quad word at the end of the bit string. The actual implementation of this operation is left as an exercise for you.
12.5 BMI1 Instructions to Extract Bits and Create Bit Masks
If your CPU supports the BMI1 (bit manipulation instructions, set 1) instruction set extensions,2 you can use the bextr (bit extraction) instruction to extract bits from a 32- or 64-bit general-purpose register. This instruction has the following syntax:
bextr regdest, regsrc, regctrl
bextr regdest, memsrc, regctrlThe operands must all be the same size and must be 32- or 64-bit registers (or memory locations).
The bextr instruction encodes two parameters into regctrl:
- Bits 0 to 7 of regctrl specify a starting bit position in the source operand (this must be a value in the range 0 to 31 for 32-bit operands and 0 to 63 for 64-bit operands).
- Bits 8 to 15 of regctrl specify the number of bits to extract from the source operand.
The bextr instruction will extract the specified bits from regsrc or memsrc and store those bits (shifted down to bit 0) in regdest. As a general rule, you should attempt to use RAX and EAX, RBX and EBX, RCX and ECX, or RDX and EDX as the ctrl register because you can easily manipulate the starting and length values by using the AH and AL, BH and BL, CH and CL, and DH and DL 8-bit registers. Listing 12-2 provides a quick demonstration of the bextr instruction.3
; Listing 12-2
; Demonstrate extracting bit strings from a register.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 12-2", 0
include getTitle.inc
include print.inc
; Here is the "asmMain" function.
.code
public asmMain
asmMain proc
push rbx
push rsi
push rdi
push rbp
mov rbp, rsp
sub rsp, 56 ; Shadow storage
; >>>> Unique code for various listings:
mov rax, 123456788abcdefh
mov bl, 4
mov bh, 16
bextr rdx, rax, rbx
call print
byte "Extracted bits: %x", nl, 0
; <<<< End of unique code.
allDone: leave
pop rdi
pop rsi
pop rbx
ret ; Returns to caller
asmMain endp
endListing 12-2: bextr instruction example
Listing 12-2 produces the following output:
C:\>build listing12-2
C:\>echo off
Assembling: listing12-2.asm
c.cpp
C:\>listing12-2
Calling Listing 12-2:
Extracted bits: bcde
Listing 12-2 terminatedThe BMI1 instruction set extension also includes an instruction that extracts the lowest-numbered set bit in a register: blsi (extract lowest set isolated bit). The syntax for this instruction is as follows:
blsi regdest, regsrc
blsi regdest, memsrcThe operands must be the same size and can be either 32 or 64 bits. This instruction locates the lowest set bit in the source operand (register or memory). It copies that bit to the destination register and zeroes out all other bits in the destination. If the source value is 0, blsi copies 0 to the destination register and sets the zero and carry flags. Listing 12-3 is a simple demonstration of this instruction (note that I’ve eliminated the common code from Listing 12-2).
; >>>> Unique code for various listings.
mov r8, 12340000h
blsi edx, r8
call print
byte "Extracted bit: %x", nl, 0
; <<<< End of unique code.Listing 12-3: Simple demonstration of the blsi instruction
Inserting this into a shell sample program and running it produces the following output:
Extracted bit: 40000The BMI1 andn instruction is useful in conjunction with blsi. The andn (and not) instruction has the following generic syntax:
andn regdest, regsrc1, regsrc2
andn regdest, regsrc1, memsrc2The operands must all be the same size and must be 32 or 64 bits. This instruction logically ANDs an inverted copy of the value in regsrc1 with the third operand (the src2 operand) and stores the result into the regdest operand.
You can use the andn instruction immediately after a blsi instruction to remove the lowest-numbered bit from blsi’s source operand after extracting it. Listing 12-4 demonstrates this operation (as usual, omitting the common code).
; >>>> Unique code for various listings.
mov r8, 12340000h
blsi edx, r8
andn r8, rdx, r8
; Output value 1 is in RDX (extracted bit),
; output value 2 in R8 (value with deleted bit).
call print
byte "Extracted bit: %x, result: %x", nl, 0
; <<<< End of unique code.Listing 12-4: Extracting and removing the lowest set bit in an operand
Running this code produces the following output:
Extracted bit: 40000, result: 12300000Extracting the LO bit and keeping the remaining bits (as was done with the blsi and andn instructions in Listing 12-4) are such a common operation that Intel created an instruction to specifically handle this task: blsr (reset lowest set bit). Here’s its generic syntax:
blsr regdest, regsrc
blsr regdest, memsrcBoth operands must be the same size and must be either 32 or 64 bits. This instruction gets the data from the source operand, sets the lowest-numbered set bit to 0, and copies the result to the destination register. If the source operand contains 0, this instruction copies 0 to the destination and sets the carry flag.
Listing 12-5 demonstrates the usage of this instruction.
; >>>> Unique code for various listings.
mov r8, 12340000h
blsr edx, r8
; Output value 1 is in RDX (extracted bit), resulting value.
call print
byte "Value with extracted bit: %x", nl, 0
; <<<< End of unique code.Listing 12-5: blsr instruction example
Here’s the output from this code fragment (after inserting it into a test program shell):
Value with extracted bit: 12300000Another useful BMI1 instruction is blsmsk. This instruction creates a bit mask by searching for the lowest-numbered set bit. Then it creates a bit mask consisting of all 1 bits up to and including the lowest set bit. The blsmsk instruction sets the remaining bits to 0. If the original value was 0, blsmsk sets all the bits in the destination register to 1 and sets the carry flag. Here’s the generic syntax for blsmsk:
blsmsk regdest, regsrc
blsmsk regdest, memsrcListing 12-6 is a sample code fragment and the output it will produce.
; >>>> Unique code for various listings.
mov r8, 12340000h
blsmsk edx, r8
; Output value 1 is in RDX (mask).
call print
byte "Mask: %x", nl, 0
; <<<< End of unique code.Listing 12-6: blsmsk example
Here is the sample output:
Mask: 7ffffEspecially note that the mask the blsmsk instruction produces includes a 1 bit in the bit position holding the lowest-numbered set bit in the source file. Often, you will actually want a bit mask containing 1 bits up to, but not including, the lowest-numbered set bit. This is easy to achieve using the blsi and dec instructions, as shown in Listing 12-7.
; >>>> Unique code for various listings.
mov r8, 12340000h
blsi rdx, r8
dec rdx
; Output value 1 is in RDX (mask).
call print
byte "Mask: %x", nl, 0
; <<<< End of unique code.Listing 12-7: Creating a bit mask that doesn’t include the lowest-numbered set bit
Here’s the output:
Mask: 3ffffThe last of the BMI1 instructions is tzcnt (trailing zero count). This instruction has the following generic syntax:
tzcnt regdest, regsrc
tzcnt regdest, memsrcAs usual, the operands must both be the same size. The tzcnt instruction is unique among the BMI1 instructions insofar as it allows 16-, 32-, and 64-bit operands.
The tzcnt instruction counts the number of LO 0 bits in the source (starting at the LO bit and working up toward the HO bit). It stores the 0 bit count into the destination register. Conveniently, the count of 0 bits is also the bit index of the first set bit in the source operand. This instruction sets the carry flag if the source operand is 0 (in which case it also sets the destination register to the size of the operands).
To search for and extract 0 bits with bextr, blsi, blsr, and blsmsk, invert the source operand before executing these instructions. Likewise, to count the number of trailing set bits with tzcnt, first invert the source operand.4
If you use bextr, blsi, blsr, blsmsk, tzcnt, or andn in your program, don’t forget to test for the presence of the BMI1 instruction set extensions. Not all x86-64 CPUs support these instructions.
12.6 Coalescing Bit Sets and Distributing Bit Strings
Inserting and extracting bit sets are only a little different from inserting and extracting bit strings if the shape of the bit set you’re inserting (or resulting bit set you’re extracting) is the same as the shape of the bit set in the main object. The shape of a bit set is the distribution of the bits in the set, ignoring the starting bit position of the set. A bit set that includes bits 0, 4, 5, 6, and 7 has the same shape as that of a bit set that includes bits 12, 16, 17, 18, and 19 because the distribution of the bits is the same.
The code to insert or extract this bit set is nearly identical to that of the previous section; the only difference is the mask value you use. For example, to insert this bit set starting at bit 0 in EAX into the corresponding bit set starting at position 12 in EBX, you could use the following code:
and ebx, not 11110001000000000000b ; Mask out destination bits
shl eax, 12 ; Move source bits into position
or ebx, eax ; Merge the bit set into EBXHowever, suppose you have 5 bits in bit positions 0 through 4 in EAX and want to merge them into bits 12, 16, 17, 18, and 19 in EBX. Somehow you have to distribute the bits in EAX prior to logically ORing the values into EBX. Given that this particular bit set is made of two runs of 1 bits, the process is somewhat simplified. The following code distributes the bits in a sneaky fashion:
and ebx, not 11110001000000000000b
and eax, 11110001000000000000b ; Mask out destination bits
shl eax, 2 ; Spread out bits: 1 to 4 goes to 3 to 6 and 0 goes to 2
btr eax, 2 ; Bit 2 -> carry and then clear bit 2
rcl eax, 13 ; Shift in carry and put bits into final position
or ebx, eax ; Merge the bit set into EBXThis trick with the btr (bit test and reset) instruction worked well because we had only 1 bit out of place in the original source operand. Alas, had the bits all been in the wrong location relative to one another, this scheme wouldn’t be an efficient solution. We’ll see a more general solution in just a moment.
Extracting this bit set and collecting (coalescing) the bits into a bit string is not quite as easy. However, we still have some sneaky tricks we can pull. Consider the following code that extracts the bit set from EBX and places the result into bits 0 to 4 of EAX:
mov eax, ebx
and eax, 11110001000000000000b ; Strip unwanted bits
shr eax, 5 ; Put bit 12 into bit 7, and so on
shr ah, 3 ; Move bits 11 to 14 to 8 to 11
shr eax, 7 ; Move down to bit 0This code moves (original) bit 12 into bit position 7, the HO bit of AL. At the same time, it moves bits 16 to 19 down to bits 11 to 14 (bits 3 to 6 of AH). Then the code shifts bits 3 to 6 in AH down to bit 0. This positions the HO bits of the bit set so that they are adjacent to the bit remaining in AL. Finally, the code shifts all the bits down to bit 0. Again, this is not a general solution, but it shows a clever way to attack this problem if you think about it carefully.
The preceding coalescence and distribution algorithms apply only to their specific bit sets. A generalized solution (perhaps one that lets you specify a mask, then distributes or coalesces the bits accordingly) is going to be a bit more difficult. The following code demonstrates how to distribute the bits in a bit string according to the values in a bit mask:
; EAX - Originally contains a value into which we
; insert bits from EBX.
; EBX - LO bits contain the values to insert into EAX.
; EDX - Bitmap with 1s indicating the bit positions in
; EAX to insert.
; CL - Scratchpad register.
mov cl, 32 ; Count number of bits we rotate
jmp DistLoop
CopyToEAX:
rcr ebx, 1 ; Don't use SHR, must preserve Z-flag
rcr eax, 1
jz Done
DistLoop: dec cl
shr edx, 1
jc CopyToEAX
ror eax, 1 ; Keep current bit in EAX
jnz DistLoop
Done: ror eax, cl ; Reposition remaining bits If we load EDX with 11001001b, this code will copy bits 0 to 3 to bits 0, 3, 6, and 7 in EAX. Notice the short-circuit test that checks whether we’ve exhausted the values in EDX (by checking for a 0 in EDX). The rotate instructions do not affect the zero flag, but the shift instructions do. Hence, the preceding shr instruction will set the zero flag when there are no more bits to distribute (when EDX becomes 0).
The general algorithm for coalescing bits is a tad more efficient than general distribution. Here’s the code that will extract bits from EBX via the bit mask in EDX and leave the result in EAX:
; EAX - Destination register.
; EBX - Source register.
; EDX - Bitmap with 1s representing bits to copy to EAX.
; EBX and EDX are not preserved.
xor eax, eax ; Clear destination register
jmp ShiftLoop
ShiftInEAX:
rcl ebx, 1 ; EBX to EAX
rcl eax, 1
ShiftLoop:
shl edx, 1 ; Check to see if we need to copy a bit
jc ShiftInEAX ; If carry set, go copy the bit
rcl ebx, 1 ; Current bit is uninteresting, skip it
jnz ShiftLoop ; Repeat as long as there are bits in EDXThis sequence also takes advantage of a sneaky trait of the shift and rotate instructions: the shift instructions affect the zero flag, whereas the rotate instructions do not. Therefore, the shl edx, 1 instruction sets the zero flag when EDX becomes 0 (after the shift). If the carry flag was also set, the code will make one additional pass through the loop in order to shift a bit into EAX, but the next time the code shifts EDX 1 bit to the left, EDX is still 0 and so the carry will be clear. On this iteration, the code falls out of the loop.
Another way to coalesce bits is via table lookup. By grabbing a byte of data at a time (so your tables don’t get too large), you can use that byte’s value as an index into a lookup table that coalesces all the bits down to bit 0. Finally, you can merge the bits at the low end of each byte together. This might produce a more efficient coalescing algorithm in certain cases. The implementation is left to you.
12.7 Coalescing and Distributing Bit Strings Using BMI2 Instructions
Intel’s BMI2 (bit manipulation instructions, set 2)5 instruction set extensions include a handy set of instructions you can use to insert or extract arbitrary bit sets: pdep (parallel bits deposit) and pext (parallel bits extract). If these instructions are available on your CPU, they can handle many of the tasks presented with non-BMI instructions in this chapter. They are powerful instructions indeed.
These instructions have the following syntax:
pdep regdest, regsrc, regmask
pdep regdest, regsrc, memmask
pext regdest, regsrc, regmask
pext regdest, regsrc, memmaskAll operands must be the same size and must be 32 or 64 bits.
The pext instruction extracts an arbitrary bit string from the source (second) register and coalesces those bits to contiguous bit locations starting at bit 0 in the destination register. The third operand, the mask, controls which bits pext extracts from the source.
The mask operand contains 1 bits in the bit positions that pext will extract from the source register. Figure 12-4 shows how this bit mask works. For each 1 bit in the mask operand, the pext instruction copies the corresponding bit in the source register to the next available bit position (starting from bit 0) in the destination register.
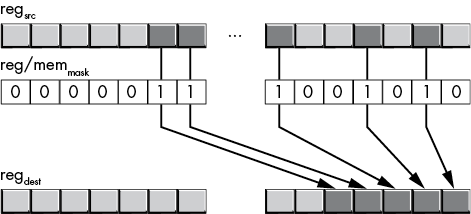
Figure 12-4: Bit mask for pext instruction
Listing 12-8 is a sample program fragment and the output it produces demonstrating the pext instruction (as usual, this listing eliminates the common code).
; >>>> Unique code for various listings.
mov r8d, 12340000h
mov r9d, 0F0f000Fh
pext edx, r8d, r9d
; Output value 1 is in RDX (mask).
call print
byte "Extracted: %x", nl, 0
; <<<< End of unique code.
------------------------------------------------------------------------------
Extracted: 240Listing 12-8: pext instruction example
The pdep instruction does the converse of pext. It takes the contiguous set of bits starting with the LO bit of the source register operand and distributes those bits throughout the destination register by using the 1 bits in the mask operand to determine placement, as shown in Figure 12-5. The pdep instruction sets all other bits in the destination register to 0.
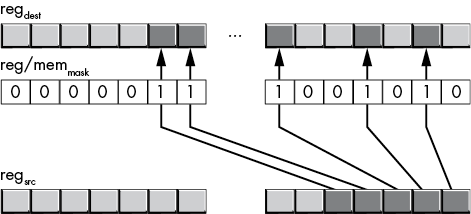
Figure 12-5: pdep instruction operation
Listing 12-9 is an example of the pdep instruction and the output it produces.
mov r8d, 1234h
mov r9d, 0F0FF00Fh
pdep edx, r8d, r9d
; Output value 1 is in RDX (mask).
call print
byte "Distributed: %x", nl, 0
------------------------------------------------------------------------------
Distributed: 1023004Listing 12-9: pdep instruction example
If you use the pdep or pext instructions in your program, don’t forget to test for the presence of the BMI2 instruction set extensions. Not all x86-64 CPUs support these instructions. See Listing 11-2 in Chapter 11 to see how to check for the presence of the BMI2 instruction set extensions.
12.8 Packed Arrays of Bit Strings
Though far less efficient, it is quite possible to create arrays of elements whose size is not a multiple of 8 bits. The drawback is that calculating the “address” of an array element and manipulating that array element involves a lot of extra work. In this section, we’ll take a look at a few examples of packing and unpacking array elements in an array whose elements are an arbitrary number of bits long.
Why would you want arrays of bit objects? The answer is simple: space. If an object consumes only 3 bits, you can get 2.67 times as many elements into the same space if you pack the data rather than allocating a whole byte for each object. For very large arrays, this can be a substantial savings. Of course, the cost of this space savings is speed: you have to execute extra instructions to pack and unpack the data, thus slowing down access to the data.
The calculation for locating the bit offset of an array element in a large block of bits is almost identical to the standard array access:
element_address_in_bits =
base_address_in_bits + index * element_size_in_bits Once you calculate the element’s address in bits, you need to convert it to a byte address (because we have to use byte addresses when accessing memory) and extract the specified element. Because the base address of an array element (almost) always starts on a byte boundary, we can use the following equations to simplify this task:
byte_of_1st_bit =
base_address + (index * element_size_in_bits) / 8
offset_to_1st_bit =
(index * element_size_in_bits) % 8For example, suppose we have an array of 200 three-bit objects that we declare as follows:
.data
AO3Bobjects byte (200 * 3)/8 + 2 dup (?) ; "+2" handles truncationThe constant expression in the preceding dimension reserves space for enough bytes to hold 600 bits (200 elements, each 3 bits long). As the comment notes, the expression adds 2 extra bytes at the end to ensure we don’t lose any odd bits6 as well as to allow us to access 1 byte beyond the end of the array (when storing data to the array).
Now suppose you want to access the ith 3-bit element of this array. You can extract these bits by using the following code:
; Extract the ith group of 3 bits in AO3Bobjects
; and leave this value in EAX.
xor ecx, ecx ; Put i / 8 remainder here
mov eax, i ; Get the index into the array
lea rax, [rax + rax * 2] ; RAX := RAX * 3 (3 bits/element)
shrd rcx, rax, 3 ; RAX / 8 -> RAX and RAX mod 8 -> RCX
; (HO bits)
shr rax, 3 ; Remember, shrd doesn't modify EAX
rol rcx, 3 ; Put remainder into LO 3 bits of RCX
; Okay, fetch the word containing the 3 bits we want to
; extract. We have to fetch a word because the last bit or two
; could wind up crossing the byte boundary (that is, bit offset 6
; and 7 in the byte).
lea r8, AO3Bobjects
mov ax, [r8][rax * 1]
shr ax, cl ; Move bits down to bit 0
and eax, 111b ; Remove the other bits (incl HO RAX)Inserting an element into the array is a bit more difficult. In addition to computing the base address and bit offset of the array element, you also have to create a mask to clear out the bits in the destination where you’re going to insert the new data. Listing 12-10 inserts the LO 3 bits of EAX into the ith element of the AO3Bobjects array.
; Listing 12-10
; Creating a bit mask with blsi and dec.
option casemap:none
nl = 10
.const
ttlStr byte "Listing 12-10", 0
Masks equ this word
word not 0111b, not 00111000b
word not 000111000000b, not 1110b
word not 01110000b, not 001110000000b
word not 00011100b, not 11100000b
.data
i dword 5
AO3Bobjects byte (200*3)/8 + 2 dup (?) ; "+2" handles truncation
include getTitle.inc
include print.inc
.code
; Here is the "asmMain" function.
public asmMain
asmMain proc
push rbx
push rsi
push rdi
push rbp
mov rbp, rsp
sub rsp, 56 ; Shadow storage
mov eax, 7 ; Value to store
mov ebx, i ; Get the index into the array
mov ecx, ebx ; Use LO 3 bits as index
and ecx, 111b ; into Masks table
lea r8, Masks
mov dx, [r8][rcx * 2] ; Get bit mask
; Convert index into the array into a bit index.
; To do this, multiply the index by 3:
lea rbx, [rbx + rbx * 2]
; Divide by 8 to get the byte index into EBX
; and the bit index (the remainder) into ECX:
shrd ecx, ebx, 3
shr ebx, 3
rol ecx, 3
; Grab the bits and clear those we're inserting.
lea r8, AO3Bobjects
and dx, [r8][rbx * 1]
; Put our 3 bits in their proper location.
shl ax, cl
; Merge bits into destination.
or dx, ax
; Store back into memory.
mov [r8][rbx * 1], dx
mov edx, dword ptr AO3Bobjects
call print
byte "value:%x", nl, 0
allDone: leave
pop rdi
pop rsi
pop rbx
ret ; Returns to caller
asmMain endp
endListing 12-10: Storing the value 7 (111b) into an array of 3-bit elements
Inserting the code in Listing 12-10 into a shell assembly file produces the following output:
value:38000The print statement prints the first 32 bits of AO3Bobjects. Because each element is 3 bits, the array looks like
000 000 000 000 000 111 000 000 000 000 00 ...where bit 0 is the leftmost bit. Flipping the 32 bits around to make them more readable, and grouping them in blocks of 4 bits (to make it easy to convert to hexadecimal), we get
0000 0000 0000 0011 1000 0000 0000 0000which is 38000h.
Listing 12-10 uses a lookup table to generate the masks needed to clear out the appropriate position in the array. Each element of this array contains all 1s except for three 0s in the position we need to clear for a given bit offset (note the use of the not operator to invert the constants in the table).
12.9 Searching for a Bit
A common bit operation is to locate the end of a run of bits. A special case of this operation is to locate the first (or last) set or clear the bit in a 16-, 32-, or 64-bit value. In this section, we’ll explore ways to handle this special case.
The term first set bit means the first bit in a value, scanning from bit 0 toward the high-order bit, which contains a 1. A similar definition exists for the first clear bit. The last set bit is the first bit in a value, scanning from the high-order bit toward bit 0, which contains a 1. A similar definition exists for the last clear bit.
One obvious way to scan for the first or last bit is to use a shift instruction in a loop and count the number of iterations before you shift out a 1 (or 0) into the carry flag. The number of iterations specifies the position. Here’s some sample code that checks for the first set bit in EAX and returns that bit position in ECX:
mov ecx, -32 ; Count off the bit positions in ECX
TstLp: shr eax, 1 ; Check to see if current bit
; position contains a 1
jc Done ; Exit loop if it does
inc ecx ; Bump up our bit counter by 1
jnz TstLp ; Exit if we execute this loop 32 times
Done: add cl, 32 ; Adjust loop counter so it holds
; the bit position
; At this point, CL contains the bit position of the
; first set bit. CL contains 32 if EAX originally
; contained 0 (no set bits). The only thing tricky about this code is that it runs the loop counter from –32 up to 0 rather than 32 down to 0. This makes it slightly easier to calculate the bit position after the loop terminates.
The drawback to this particular loop is that it’s expensive. This loop repeats as many as 32 times, depending on the original value in EAX. If the values you’re checking often have lots of 0s in the LO bits of EAX, this code runs rather slowly.
Searching for the first (or last) set bit is such a common operation that Intel added a couple of instructions specifically to accelerate this process. These instructions are bsf (bit scan forward) and bsr (bit scan reverse). Their syntax is as follows:
bsr destreg, regsrc
bsr destreg, memsrc
bsf destreg, regsrc
bsf destreg, memsrc The source and destination operands must be the same size (16, 32, or 64 bits). The destination operand has to be a register. The source operand can be a register or a memory location.
The bsf instruction scans for the first set bit (starting from bit position 0) in the source operand. The bsr instruction scans for the last set bit in the source operand by scanning from the HO bit toward the LO bit. If these instructions find a bit that is set in the source operand, they clear the zero flag and put the bit position into the destination register. If the source register contains 0 (that is, there are no set bits), then these instructions set the zero flag and leave an indeterminate value in the destination register. You should test the zero flag immediately after the execution of these instructions to validate the destination register’s value. Here’s an example:
mov ebx, SomeValue ; Value whose bits we want to check
bsf eax, ebx ; Put position of first set bit in EAX
jz NoBitsSet ; Branch if SomeValue contains 0
mov FirstBit, eax ; Save location of first set bit
.
.
.You use the bsr instruction in an identical fashion except that it computes the bit position of the last set bit in an operand (the first set bit it finds when scanning from the HO bit toward the LO bit).
The x86-64 CPUs do not provide instructions to locate the first bit containing a 0. However, you can easily scan for a 0 bit by first inverting the source operand (or a copy of the source operand if you must preserve the source operand’s value) and then searching for the first 1 bit; this corresponds to the first 0 bit in the original operand value.
The bsf and bsr instructions are complex x86-64 instructions and may be slower than others. In some circumstances, it may be faster to locate the first set bit by using discrete instructions. However, because the execution time of these instructions varies widely from CPU to CPU, you should test the performance of these instructions prior to using them in time-critical code.
Note that the bsf and bsr instructions do not affect the source operand. A common operation is to extract (and clear) the first or last set bit you find in an operand. If the source operand is in a register, you can use the btr (or btc) instruction to clear the bit after you’ve found it. Here’s some code that achieves this result:
bsf ecx, eax ; Locate first set bit in EAX
jz noBitFound ; If we found a bit, clear it
btr eax, ecx ; Clear the bit we just found
noBitFound: At the end of this sequence, the zero flag indicates whether we found a bit (note that btr doesn’t affect the zero flag).
Because the bsf and bsr instructions support only 16-, 32-, and 64-bit operands, you will have to compute the first bit position of an 8-bit operand a little differently. There are a couple of reasonable approaches. First, you can zero-extend an 8-bit operand to 16 or 32 bits and then use the bsf or bsr instruction. Another alternative is to create a lookup table in which each entry contains the number of bits in the value you use as an index into the table; then you can use the xlat instruction to “compute” the first bit position in the value (you will have to handle the value 0 as a special case). Another solution is to use the shift algorithm appearing at the beginning of this section; for an 8-bit operand, this is not an entirely inefficient solution.
You can use bsf and bsr to determine the size of a run of bits, assuming that you have a single run of bits in your operand. Simply locate the first and last bits in the run (as in the previous example) and then compute the difference (plus 1) of the two values. Of course, this scheme is valid only if there are no intervening 0s between the first and last set bits in the value.
12.10 Counting Bits
The last example in the previous section demonstrates a specific case of a very general problem: counting bits. Unfortunately, that example has a severe limitation: it counts only a single run of 1 bits appearing in the source operand. This section discusses a more general solution to this problem.
Hardly a week goes by that someone doesn’t ask on one of the internet newsgroups how to count the number of bits in a register operand. This is a common request, undoubtedly because many assembly language course instructors assign this task as a project to their students as a way to teach them about the shift and rotate instructions, as follows:
; BitCount1:
; Counts the bits in the EAX register,
; returning the count in EBX.
mov cl, 32 ; Count the 32 bits in EAX
xor ebx, ebx ; Accumulate the count here
CntLoop: shr eax, 1 ; Shift bit out of EAX and into carry
adc bl, 0 ; Add the carry into the EBX register
dec cl ; Repeat 32 times
jnz CntLoop The “trick” is that this code uses the adc instruction to add the value of the carry flag into the BL register. Because the count is going to be less than 32, the result will fit comfortably into BL.
Tricky code or not, this instruction sequence is not particularly fast. The preceding loop always executes 32 times, so this code sequence executes 130 instructions (four instructions per iteration plus two extra instructions).
For a more efficient solution, use the popcnt instruction (population count, introduced in the SSE 4.1 instruction set), which counts the number of 1 bits in the source operand and stores the value into the destination operand:
popcnt regdest, regsrc
popcnt regdest, memsrcThe operands must be the same size and must be 16, 32, or 64 bits.
12.11 Reversing a Bit String
Another common programming project instructors assign, and a useful function in its own right, is a program that reverses the bits in an operand. This program swaps the LO bit with the HO bit, bit 1 with the next-to-HO bit, and so on. The typical solution an instructor expects is the following:
; Reverse the 32 bits in EAX, leaving the result in EBX:
mov cl, 32 ; Move current bit in EAX to
RvsLoop: shr eax, 1 ; the carry flag
rcl ebx, 1 ; Shift the bit back into
; EBX, backward
dec cl
jnz RvsLoop As with the previous examples, this code suffers from repeating the loop 32 times, for a grand total of 129 instructions (for 32-bit operands, so double that for 64-bit operands). By unrolling the loop, you can get it down to 64 instructions, but this is still somewhat expensive.
The best solution to an optimization problem is often using a better algorithm rather than attempting to tweak your code by trying to choose faster instructions to speed it up. In the preceding section, for example, we were able to speed up counting the bits in a string by substituting a more complex algorithm for the simplistic “shift and count” algorithm. In the preceding example, the trick is to do as much work as possible in parallel.
Suppose that all we wanted to do was swap the even and odd bits in a 32-bit value. We can easily swap the even and odd bits in EAX by using the following code:
mov edx, eax ; Make a copy of the odd bits
shr eax, 1 ; Move the even bits to the odd positions
and edx, 55555555h ; Isolate the odd bits
and eax, 55555555h ; Isolate the even bits
shl edx, 1 ; Move the odd bits to even positions
or eax, edx ; Merge the bits and complete the swapSwapping the even and odd bits takes us part of the way to reversing all the bits in the number. After executing the preceding code sequence, you can swap adjacent pairs of bits to swap the bits in all the nibbles in the 32-bit value by using the following code:
mov edx, eax ; Make a copy of the odd-numbered bit pairs
shr eax, 2 ; Move the even bit pairs to the odd position
and edx, 33333333h ; Isolate the odd pairs
and eax, 33333333h ; Isolate the even pairs
shl edx, 2 ; Move the odd pairs to the even positions
or eax, edx ; Merge the bits and complete the swapAfter completing the preceding sequence, you swap the adjacent nibbles in the 32-bit register. Again, the only difference is the bit mask and the length of the shifts. Here’s the code:
mov edx, eax ; Make a copy of the odd-numbered nibbles
shr eax, 4 ; Move the even nibbles to the odd position
and edx, 0f0f0f0fh ; Isolate the odd nibbles
and eax, 0f0f0f0fh ; Isolate the even nibbles
shl edx, 4 ; Move the odd pairs to the even positions
or eax, edx ; Merge the bits and complete the swapYou can probably see the pattern developing and can figure out that in the next two steps you have to swap the bytes and then the words in this object. You can use code like the preceding example, but there is a better way: use bswap. The bswap (byte swap) instruction uses the following syntax:
bswap reg32 The bswap instruction swaps bytes 0 and 3 and bytes 1 and 2 in the specified 32-bit register, exactly what you want when reversing bits (and when converting data between little-endian and big-endian data formats, the principal use of this instruction). Rather than sticking in another 12 instructions to swap the bytes and then the words, you can simply use a bswap eax instruction to complete the job after the preceding instructions. The final code sequence is shown here:
mov edx, eax ; Make a copy of the odd bits in the data
shr eax, 1 ; Move the even bits to the odd positions
and edx, 55555555h ; Isolate the odd bits
and eax, 55555555h ; Isolate the even bits
shl edx, 1 ; Move the odd bits to the even positions
or eax, edx ; Merge the bits and complete the swap
mov edx, eax ; Make a copy of the odd-numbered bit pairs
shr eax, 2 ; Move the even bit pairs to the odd position
and edx, 33333333h ; Isolate the odd pairs
and eax, 33333333h ; Isolate the even pairs
shl edx, 2 ; Move the odd pairs to the even positions
or eax, edx ; Merge the bits and complete the swap
mov edx, eax ; Make a copy of the odd-numbered nibbles
shr eax, 4 ; Move the even nibbles to the odd position
and edx, 0f0f0f0fh ; Isolate the odd nibbles
and eax, 0f0f0f0fh ; Isolate the even nibbles
shl edx, 4 ; Move the odd pairs to the even positions
or eax,edx ; Merge the bits and complete the swap
bswap eax ; Swap the bytes and wordsThis algorithm requires only 19 instructions and executes much faster than does the bit-shifting loop appearing earlier. Of course, this sequence does consume a little more memory. If you’re trying to save memory rather than clock cycles, the loop is probably a better solution.
12.12 Merging Bit Strings
Another common bit string operation is producing a single bit string by merging, or interleaving, bits from two different sources. The following example code sequence creates a 32-bit string by merging alternate bits from two 16-bit strings:
; Merge two 16-bit strings into a single 32-bit string.
; AX - Source for even-numbered bits.
; BX - Source for odd-numbered bits.
; CL - Scratch register.
; EDX - Destination register.
mov cl, 16
MergeLp: shrd edx, eax, 1 ; Shift a bit from EAX into EDX
shrd edx, ebx, 1 ; Shift a bit from EBX into EDX
dec cl
jne MergeLp; This particular example merges two 16-bit values together, alternating their bits in the result value. For a faster implementation of this code, unroll the loop to eliminate half the instructions.
With a few slight modifications, we can merge four 8-bit values together, or merge other bit sets from the source strings. For example, the following code copies bits 0 to 5 from EAX, then bits 0 to 4 from EBX, then bits 6 to 11 from EAX, then bits 5 to 15 from EBX, and finally bits 12 to 15 from EAX:
shrd edx, eax, 6
shrd edx, ebx, 5
shrd edx, eax, 6
shrd edx, ebx, 11
shrd edx, eax, 4Of course, if you have BMI2 instructions available, you can also use the pextr instruction to extract various bits for insertion into another register.
12.13 Extracting Bit Strings
We can also extract and distribute bits in a bit string among multiple destinations. The following code takes the 32-bit value in EAX and distributes alternate bits among the BX and DX registers:
mov cl, 16 ; Count the loop iterations
ExtractLp: shr eax, 1 ; Extract even bits to (E)BX
rcr ebx, 1
shr eax, 1 ; Extract odd bits to (E)DX
rcr edx, 1
dec cl ; Repeat 16 times
jnz ExtractLp
shr ebx, 16 ; Need to move the results from the HO
shr edx, 16 ; bytes of EBX and EDX to the LO bytesThis sequence executes 99 instructions (six inside the loop repeated 16 times plus three outside the loop). You can unroll the loop and pull other tricks, but it’s probably not worth the added complexity when it’s all said and done.
If you have the BMI2 instruction set extensions available, you can also use the pext instruction to do this job efficiently:
mov ecx, 55555555h ; Odd bit positions
pext edx, eax, ecx ; Put odd bits into EDX
mov ecx, 0aaaaaaaah ; Even bit positions
pext ebx, eax, ecx ; Put even bits into EBX12.14 Searching for a Bit Pattern
Another bit-related operation you may need is the ability to search for a particular bit pattern in a string of bits. For example, you might want to locate the bit index of the first occurrence of 1011b starting at some particular position in a bit string. In this section, we’ll explore some simple algorithms to accomplish this task.
To search for a particular bit pattern, we need to know four things:
- The pattern to search for (the pattern)
- The length of the pattern we’re searching for
- The bit string that we’re going to search through (the source)
- The length of the bit string to search through
The basic idea behind the search is to create a mask based on the length of the pattern and mask a copy of the source with this value. Then we can directly compare the pattern with the masked source for equality. If they are equal, you’re finished; if they’re not equal, increment a bit position counter, shift the source one position to the right, and try again. You repeat this operation length(source) - length(pattern) times. The algorithm fails if it does not detect the bit pattern after this many attempts (because we will have exhausted all the bits in the source operand that could match the pattern’s length). Here’s a simple algorithm that searches for a 4-bit pattern throughout the EBX register:
mov cl, 28 ; 28 attempts because 32 - 4 = 28
; (len(src) - len(pat))
mov ch, 1111b ; Mask for the comparison
mov al, pattern ; Pattern to search for
and al, ch ; Mask unnecessary bits in AL
mov ebx, source ; Get the source value
ScanLp: mov dl, bl ; Copy the LO 4 bits of EBX
and dl, ch ; Mask unwanted bits
cmp al, dl ; See if we match the pattern
jz Matched
dec cl ; Repeat specified number of times
shr ebx, 1
jnz ScanLp
; Do whatever needs to be done if we failed to
; match the bit string.
jmp Done
Matched:
; If we get to this point, we matched the bit string.
; We can compute the position in the original source as 28 - CL.
Done: Bit-string scanning is a special case of string matching. String matching is a well-studied problem in computer science, and many of the algorithms you can use for string matching are applicable to bit-string matching as well. Such algorithms are beyond the scope of this chapter, but to give you a preview of how this works, you compute a function (like xor or sub) between the pattern and the current source bits and use the result as an index into a lookup table to determine how many bits you can skip. Such algorithms let you skip several bits rather than shifting only once for each iteration of the scanning loop (as is done by the previous algorithm).
12.15 For More Information
The AMD Athlon optimization guide contains useful algorithms for bit-based computations. To learn more about bit-searching algorithms, pick up a textbook on data structures and algorithms and study the section on string-matching algorithms.
Probably the ultimate book on bit twiddling is Hacker’s Delight, Second Edition, by Henry S. Warren (Addison-Wesley, 2012). While this book uses the C programming language for examples, almost all the concepts apply to assembly language programs as well.
12.16 Test Yourself
- What general instruction(s) would you use to clear bits in a register?
- What instruction could you use to clear a bit, specified by bit number, in a register?
- What general instruction would you use to set bits in a register?
- What instruction could you use to set a bit, specified by bit number, in a register?
- What general instruction would you use to invert bits in a register?
- What instruction could you use to invert a bit, specified by bit number, in a register?
- What general instruction would you use to test a bit (or group of bits) for 0 and 1 in a register?
- What instruction could you use to test a single bit, specified by bit number, in a register?
- What single instruction could you use to extract and coalesce a set of bits?
- What single instruction could you use to position and insert a set of bits in a register?
- What single instruction could you use to extract a bit substring from a larger bit string?
- What instruction allows you to search for the first set bit in a register?
- What instruction allows you to search for the last set bit in a register?
- How would you search for the first clear bit in a register?
- How would you search for the last clear bit in a register?
- What instruction can you use to count the number of bits in a register?