第四章：案例研究：接口设计

本章将通过一个案例研究，介绍如何设计出相互配合的函数。

本章会介绍 turtle 模块，它可以让你使用海龟图形（turtle graphics）绘制图像。大部分的Python安装环境下都包含了这个模块，但是如果你是在PythonAnywhere上运行Python的，你将无法运行本章中的代码示例（至少在我写这章时是做不到的）。

如果你已经在自己的电脑上安装了Python，那么不会有问题。如果没有，现在就是安装Python的好时机。我在 http://tinyurl.com/thinkpython2e 这个页面上发布了相关指南。

本章的示例代码可以从http://thinkpython2.com/code/polygon.py 获得。

turtle模块

打开Python解释器，输入以下代码，检查你是否安装了 turltle 模块：

>>> import turtle
>>> bob = turtle.Turtle()

上述代码运行后，应该会新建一个窗口，窗口中间有一个小箭头，代表的就是海龟。现在关闭窗口。

新建一个名叫 mypolygon.py 的文件，输入以下代码：

import turtle
bob = turtle.Turtle()
print(bob)
turtle.mainloop()

turtle 模块（小写的t）提供了一个叫作 Turtle 的函数（大写的T），这个函数会创建一个 Turtle 对象，我们将其赋值给名为 bob 的变量。打印 bob 的话，会输出下面这样的结果：

<turtle.Turtle object at 0xb7bfbf4c>

这意味着，bob 指向一个类型为Turtle的对象，这个类型是由 turtle 模块定义的。

mainloop 告诉窗口等待用户操作，尽管在这个例子中，用户除了关闭窗口之外，并没有其他可做的事情。

创建了一个 Turtle 对象之后，你可以调用 方法（method） 来在窗口中移动该对象。方法与函数类似，但是其语法略有不同。例如，要让海龟向前走：

bob.fd(100)

方法 fd 与我们称之为 bob 的对象是相关联的。调用方法就像提出一个请求：你在请求 bob 往前走。

fd 方法的实参是像素距离，所以实际前进的距离取决于你的屏幕。

Turtle 对象中你能调用的其他方法还包括：让它向后走的 bk ，向左转的 lt ，向右转的 rt 。 lt 和 rt 这两个方法接受的实参是角度。

另外，每个 Turtle 都握着一支笔，不是落笔就是抬笔；如果落笔了，Turtle 就会在移动时留下痕迹。pu 和 pd 这两个方法分别代表“抬笔（pen up）”和“落笔（pen down）”。

如果要画一个直角（right angle），请在程序中添加以下代码（放在创建 bob 之后，调用 mainloop 之前）：

bob.fd(100)
bob.lt(90)
bob.fd(100)

当你运行此程序时，你应该会看到 bob 先朝东移动，然后向北移动，同时在身后留下两条线段（line segment）。

现在修改程序，画一个正方形。在没有成功之前，不要继续往下看。

简单的重复

很有可能你刚才写了像下面这样的一个程序：

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)

我们可以利用一个 for 语句，以更简洁的代码来做相同的事情。将下面的示例代码加入 mypolygon.py ，并重新运行：

for i in range(4):
    print('Hello!')

你应该会看到如下输出：

Hello!
Hello!
Hello!
Hello!

这是 for 语句最简单的用法；后面我们会介绍更多的用法。但是这对于让你重写画正方形的程序已经足够了。如果没有完成，请不要往下看。

下面是一个画正方形的 for 语句：

for i in range(4):
    bob.fd(100)
    bob.lt(90)

for语句的语法和函数定义类似。它有一个以冒号结尾的语句头（header）以及一个缩进的语句体（body）。语句体可以包含任意条语句。

for 语句有时也被称为循环（loop），因为执行流程会贯穿整个语句体，然后再循环回顶部。在此例中，它将运行语句体四次。

这个版本事实上和前面画正方形的代码有所不同，因为它在画完正方形的最后一条边后，又多转了一下。这个额外的转动多花了些时间，但是如果我们每次都通过循环来做这件事情，这样反而是简化了代码。这个版本还让海龟回到了初始位置，朝向也与出发时一致。

练习

下面是一系列学习使用 Turtle 的练习。这些练习虽说是为了好玩，但是也有自己的目的。你在做这些练习的时候，想一想它们的目的是什么。

译者注：原文中使用的还是 TurtleWorld ，应该是作者忘了修改。

后面几节中介绍了这些练习的答案，因此如果你还没完成（或者至少试过），请不要看答案。

写一个名为 square 的函数，接受一个名为 t 的形参，t 是一个海龟。这个函数应用这只海龟画一个正方形。

写一个函数调用，将 bob 作为实参传给 square ，然后再重新运行程序。
给 square 增加另一个名为 length 的形参。修改函数体，使得正方形边的长度是 length ，然后修改函数调用，提供第二个实参。重新运行程序。用一系列 length 值测试你的程序。
复制 square ，并将函数改名为 polygon 。增加另外一个名为 n 的形参并修改函数体，让它画一个正n边形（n-sided regular polygon）。提示：正n边形的外角是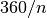 $360/n$ 度。
编写一个名为 circle 的函数，它接受一个海龟t和半径r作为形参，然后以合适的边长和边数调用 polygon ，画一个近似圆形。用一系列r值测试你的函数。

提示：算出圆的周长，并确保 length * n = circumference 。
完成一个更泛化（general）的 circle 函数，称其为 arc ，接受一个额外的参数 angle ，确定画多完整的圆。angle 的单位是度，因此当 angle=360 时， arc 应该画一个完整的圆。

封装

第一个练习要求你将画正方形的代码放到一个函数定义中,然后调用该函数，将海龟作为形参传递给它。下面是一个解法：

def square(t):
    for i in range(4):
        t.fd(100)
        t.lt(90)

square(bob)

最内层的语句 fd 和 lt 被缩进两次，以显示它们处在 for 循环内，而该循环又在函数定义内。下一行 square(bob) 和左边界（left margin）对齐，表示 for 循环和函数定义结束。

在函数内部，t 指的是同一只海龟 bob ，所以 t.lt(90) 和 bob.lt(90) 的效果相同。那么既然这样，为什么不将形参命名为 bob 呢？因为 t 可以是任何海龟而不仅仅是 bob ，也就是说你可以创建第二只海龟，并且将它作为实参传递给 square ：

alice = Turtle()
square(alice)

将一部分代码包装在函数里被称作 encapsulation（封装）。封装的好处之一，为这些代码赋予一个名字，这充当了某种文档说明。另一个好处是，如果你重复使用这些代码，调用函数两次比拷贝粘贴函数体要更加简洁！

泛化

下一个练习是给 square 增加一个 length 形参。下面是一个解法：

def square(t, length):
    for i in range(4):
        t.fd(length)
        t.lt(90)

square(bob, 100)

为函数增加一个形参被称作泛化（generalization），因为这使得函数更通用：在前面的版本中，正方形的边长总是一样的；此版本中，它可以是任意大小。

下一个练习也是泛化。泛化之后不再是只能画一个正方形，polygon 可以画任意的正多边形。下面是一个解法：

def polygon(t, n, length):
    angle = 360 / n
    for i in range(n):
        t.fd(length)
        t.lt(angle)

polygon(bob, 7, 70)

这个示例代码画了一个边长为70的七边形。

如果你在使用Python 2，angle 的值可能由于整型数除法（integer division）出现偏差。一个简单的解决办法是这样计算 angle ：angle = 360.0 / n。因为分子（numerator）是一个浮点数，最终的结果也会是一个浮点数。

如果一个函数有几个数字实参，很容易忘记它们是什么或者它们的顺序。在这种情况下，在实参列表中加入形参的名称是通常是一个很好的办法：

polygon(bob, n=7, length=70)

这些被称作关键字实参（keyword arguments），因为它们加上了形参名作为“关键字”（不要和Python的关键字搞混了，如 while 和 def ）。

这一语法使得程序的可读性更强。它也提醒了我们实参和形参的工作方式：当你调用函数时，实参被赋给形参。

接口设计

下一个练习是编写接受半径r作为形参的 circle 函数。下面是一个使用 polygon 画一个50边形的简单解法：

import math

def circle(t, r):
    circumference = 2 * math.pi * r
    n = 50
    length = circumference / n
    polygon(t, n, length)

函数的第一行通过半径r计算圆的周长，公式是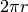 $2 \pi r$ 。由于用了 math.pi ，我们需要导入 math 模块。按照惯例，import 语句通常位于脚本的开始位置。

n是我们的近似圆中线段的条数， length 是每一条线段的长度。这样 polygon 画出的就是一个50边形，近似一个半径为r的圆。

这种解法的一个局限在于，n是一个常量，意味着对于非常大的圆，线段会非常长，而对于小圆，我们会浪费时间画非常小的线段。一个解决方案是将n作为形参，泛化函数。这将给用户（调用 circle 的人）更多的掌控力，但是接口就不那么干净了。

函数的接口（interface）是一份关于如何使用该函数的总结：形参是什么？函数做什么？返回值是什么？如果接口让调用者避免处理不必要的细节，直接做自己想做的事，那么这个接口就是“干净的”。

在这个例子中，r 属于接口的一部分，因为它指定了要画多大的圆。 n就不太合适，因为它是关于如何画圆的细节。

与其把接口弄乱，不如根据周长（circumference）选择一个合适的n值：

def circle(t, r):
    circumference = 2 * math.pi * r
    n = int(circumference / 3) + 1
    length = circumference / n
    polygon(t, n, length)

现在线段的数量，是约为周长三分之一的整型数，所以每条线段的长度（大概）是3，小到足以使圆看上去逼真，又大到效率足够高，对任意大小的圆都能接受。

重构

当我写 circle 程序的时候，我能够复用 polygon ，因为一个多边形是与圆形非常近似。但是 arc 就不那么容易实现了；我们不能使用 polygon 或者 circle 来画一个弧。

一种替代方案是从复制 polygon 开始，然后将它转化为 arc 。最后的函数看上去可像这样：

def arc(t, r, angle):
    arc_length = 2 * math.pi * r * angle / 360
    n = int(arc_length / 3) + 1
    step_length = arc_length / n
    step_angle = angle / n

    for i in range(n):
        t.fd(step_length)
        t.lt(step_angle)

该函数的后半部分看上去很像 polygon ，但是在不改变接口的条件下，我们无法复用 polygon 。我们可以泛化 polygon 来接受一个角度作为第三个实参，但是这样 polygon 就不再是一个合适的名字了！让我们称这个更通用的函数为 polyline ：

def polyline(t, n, length, angle):
    for i in range(n):
        t.fd(length)
        t.lt(angle)

现在，我们可以用 polyline 重写 polygon 和 arc ：

def polygon(t, n, length):
    angle = 360.0 / n
    polyline(t, n, length, angle)

def arc(t, r, angle):
    arc_length = 2 * math.pi * r * angle / 360
    n = int(arc_length / 3) + 1
    step_length = arc_length / n
    step_angle = float(angle) / n
    polyline(t, n, step_length, step_angle)

最后，我们可以用 arc 重写 circle ：

def circle(t, r):
    arc(t, r, 360)

重新整理一个程序以改进函数接口和促进代码复用的这个过程，被称作重构（refactoring）。在此例中，我们注意到 arc 和 polygon 中有相似的代码，因此，我们“将它分解出来”（factor it out），放入 polyline 函数。

如果我们提前已经计划好了，我们可能会首先写 polyline 函数，避免重构，但是在一个项目开始的时候，你常常并不知道那么多，不能设计好全部的接口。一旦你开始编码后，你才能更好地理解问题。有时重构是一个说明你已经学到某些东西的预兆。

开发方案

开发计划（development plan）是一种编写程序的过程。此例中我们使用的过程是“封装和泛化”。这个过程的具体步骤是：

从写一个没有函数定义的小程序开始。
一旦该程序运行正常，找出其中相关性强的部分，将它们封装进一个函数并给它一个名字。
通过增加适当的形参，泛化该函数。
重复1–3步，直到你有一些可正常运行的函数。复制粘贴有用的代码，避免重复输入（和重新调试）。
寻找机会通过重构改进程序。例如，如果在多个地方有相似的代码，考虑将它分解到一个合适的通用函数中。

这个过程也有一些缺点。后面我们将介绍其他替代方案，但是如果你事先不知道如何将程序分解为函数，这是个很有用办法。该方法可以让你一边编程，一边设计。

文档字符串

文档字符串（docstring）是位于函数开始位置的一个字符串，解释了函数的接口（“doc”是“documentation”的缩写）。下面是一个例子：

def polyline(t, n, length, angle):
    """Draws n line segments with the given length and
    angle (in degrees) between them.  t is a turtle.
    """
    for i in range(n):
        t.fd(length)
        t.lt(angle)

按照惯例，所有的文档字符串都是三重引号（triple-quoted）字符串，也被称为多行字符串，因为三重引号允许字符串超过一行。

它很简要（terse），但是包括了他人使用此函数时需要了解的关键信息。它扼要地说明该函数做什么（不介绍背后的具体细节）。它解释了每个形参对函数的行为有什么影响，以及每个形参应有的类型（如果它不明显的话）。

写这种文档是接口设计中很重要的一部分。一个设计良好的接口应该很容易解释，如果你很难解释你的某个函数，那么你的接口也许还有改进空间。

调试

接口就像是函数和调用者之间的合同。调用者同意提供合适的参数，函数同意完成相应的工作。

例如，polyline 函数需要4个实参：t 必须是一个 Turtle ； n 必须是一个整型数； length 应该是一个正数； angle 必须是一个数，单位是度数。

这些要求被称作先决条件（preconditions），因为它们应当在函数开始执行之前成立（true）。相反，函数结束时的条件是后置条件（postconditions）。后置条件包括函数预期的效果（如画线段）以及任何其他附带效果（如移动 Turtle 或者做其它改变）。

先决条件由调用者负责满足。如果调用者违反一个（已经充分记录文档的！）先决条件，导致函数没有正确工作，则故障（bug）出现在调用者一方，而不是函数。

如果满足了先决条件，没有满足后置条件，故障就在函数一方。如果你的先决条件和后置条件都很清楚，将有助于调试。

术语表

方法（method）：

与对象相关联的函数，并使用点标记法（dot notation）调用。

循环（loop）：

程序中能够重复执行的那部分代码。

封装（encapsulation）：

将一个语句序列转换成函数定义的过程。

泛化（generalization）：

使用某种可以算是比较通用的东西（像变量和形参），替代某些没必要那么具体的东西（像一个数字）的过程。

关键字实参（keyword argument）：

包括了形参名称作为“关键字”的实参。

接口（interface）：

对如何使用一个函数的描述，包括函数名、参数说明和返回值。

重构（refactoring）：

修改一个正常运行的函数，改善函数接口及其他方面代码质量的过程。

开发计划（development plan）：

编写程序的一种过程。

文档字符串（docstring）：

出现在函数定义顶部的一个字符串，用于记录函数的接口。

先决条件（preconditions）：

在函数运行之前，调用者应该满足的要求。 ends.

后置条件（postconditions）：

函数终止之前应该满足的条件。

练习题

习题 4-1

可从http://thinkpython2.com/code/polygon.py 下载本章的代码。

画一个执行 circle(bob, radius) 时的堆栈图（stack diagram），说明程序的各个状态。你可以手动进行计算，也可以在代码中加入打印语句。
“重构”一节中给出的 arc 函数版本并不太精确，因为圆形的线性近似（linear approximation）永远处在真正的圆形之外。因此，Turtle 总是和正确的终点相差几个像素。我的答案中展示了降低这个错误影响的一种方法。阅读其中的代码，看看你是否能够理解。如果你画一个堆栈图的话，你可能会更容易明白背后的原理。

习题 4-2

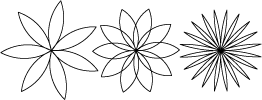
图4-1：使用Turtle绘制的花朵。

编写比较通用的一个可以画出像图4-1中那样花朵的函数集。

答案： http://thinkpython2.com/code/flower.py ，还要求使用这个模块 http://thinkpython2.com/code/polygon.py.

习题 4-3

图4-2：使用Turtle画的饼状图。

编写比较通用的一个可以画出图4-2中那样图形的函数集，。

答案： http://thinkpython2.com/code/pie.py 。

习题 4-4

字母表中的字母可以由少量基本元素构成，例如竖线和横线，以及一些曲线。设计一种可用由最少的基本元素绘制出的字母表，然后编写能画出各个字母的函数。

你应该为每个字母写一个函数，起名为draw_a，draw_b等等，然后将你的函数放在一个名为 letters.py 的文件里。你可以从http://thinkpython2.com/code/typewriter.py 下载一个“海龟打字员”来帮你测试代码。

你可以在 http://thinkpython2.com/code/letters.py 中找到答案；这个解法还要求使用 http://thinkpython2.com/code/polygon.py 。

习题 4-5

前往http://en.wikipedia.org/wiki/Spiral 阅读螺线（spiral）的相关知识；然后编写一个绘制阿基米德螺线（或者其他种类的螺线）的程序。

答案：http://thinkpython2.com/code/spiral.py 。

贡献者

翻译：@bingjin
校对：@bingjin
参考：@carfly